고체역학에서는 역학적 평형 상태에 있는 고체의 변형/고체의 각 부분에 걸린 부하를 보는 것을 목표로 합니다. 외력을 강하게 전달한다 하더라도 그 외력을 받는 고체가 매우 크게 되면 단위 면적당 가해지는 힘$(P/A)$은 그리 크지 않게 되고, 변형된 길이가 크더라도 원래 고체의 길이 자체가 매우 컸다면, 단위 길이당 변형된 길이$(\delta/L)$는 그닥 큰 값이 아니게 됩니다. 즉, 중요한것은 적대적은 힘, 변형의 크기가 아닌 그 비율을 보는 것이 중요하다는 것을 알수 있습니다. 이러한 맥락에서 stress, strain이라는 것을 도입하였고, 아래에서 알아볼 것입니다.
$\cdot$Stress(응력)
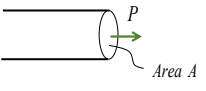
Stress, 응력이란 외부에서 힘이 가해질 때 그 크기에 대응하여 내부에 생기는 저항력을 의미한다. 대표적인 예시로, 단단한 막대를 $P$의 힘으로 잡아 늘인다고 생각해보자. 그러면 그 막대는 늘어나지 않기 위해서 내부에 힘이 생길 것이다. 그것이 바로 응력인 것이다. 위에서, 우리는 stress가 단위면적당 힘이라고 하였습니다. 즉, 잡아당긴 잡아당긴 방향과 수직한 단면에서 보았을 때, 우리는 stress $\sigma = \frac{P}{A}$라고 할 수 있다. 그리고 문체 내부에 생긴 이 응력은 우리가 잡은 단면과 수직한 방향으로 생긴다. 우리는 이것을 normal stress라고 한다.
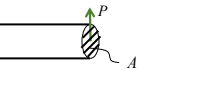
이번엔, 바닥에 고정된 직육면체 블록의 윗면을 잡고 바닥면과 나란한 방향으로 당겨보자. 이번에는 윗면과 평행한 단면을 잘랐을 떄, normal stress가 존재하지 않는다. 그렇지만, 이 블록이 형체를 유지하기 위한 내부의 힘은 반드시 존재해야 한다. 이때, 그 정체가 바로 shear stress라고 하며, 단면에 수직한 방향으로 생기는 stress이다.
Normal stress와 shear stress는 아래와 같다.
Normal stress$\sigma=\frac{P}{A}$
Shear stress$\tau=\frac{P}{A}$
이번엔 아까의 단면을 여러 방법으로 자를 때 어떻게 되는지를 알아보자. 단면을 어떻게 생각하느냐에 따라서 normal stress와 shear stress가 다르게 나올 것이다. 아래의 그림을 보자.
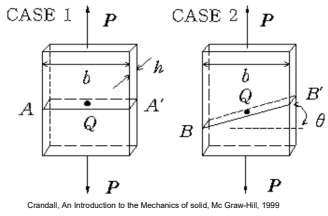
물체를 위아래로 $P$의 힘으로 잡아당기고 있는 상황에서, 하나는 힘의 방향헤 수직한 면을 잡아보았고, 나머지 하나는 $\theta$만큼 기울어진 면을 단면으로 잡았다. 왼쪽 그림의 단면의 경우 아까와 같은 상황이므로 아래와 같은 결과를 얻는다.
$$\sigma=\frac{P}{bh}, \tau=0$$
그러나, 비스듬히 단면을 잡으면 단면과 수직한 성분과 단면에 평행한 성분의 합력이 P를 만들어내야 하므로, 아래와 같은 결과를 얻을 것이다.
$$\sigma=\frac{P}{bh}\cos^2 \theta, \tau=\frac{P}{bh}\sin \theta \cos \theta$$
즉, stress는 단면의 방향까지 정해야 완전히 정의할 수 있는 것이다.
Stress는 물체의 각 지점마다 정의되는 물리량이다. 그렇다면, stress는 벡터인 힘에 대해서 정의한 물리량이니까 3차원 벡터인가? 답은 No이다. Catesian coordinate에서 stress는 총 9가지가 존재한다. 법선벡터가 x, y, z축 방향인 3가지 면의 방향이 존재할 것이고, 각 면마다 x, y, z방향으로 3가지 방향의 stress가 있을 것이다. 즉, 응력은 총 9가지 성분으로 이루어져있으며, 이는 3$\times$3 matrix로 나타낼 수 있는 2차 텐서이다.
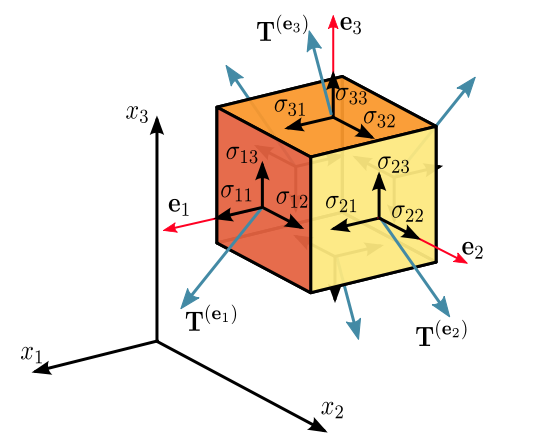
$$\boldsymbol{\sigma} = \begin{pmatrix} \sigma_{11} & \sigma_{12} & \sigma_{13} \\\\ \sigma_{21} & \sigma_{22} & \sigma_{23} \\\\ \sigma_{31} & \sigma_{32} & \sigma_{33} \end{pmatrix}$$
Stress tensor는 위와 같이 나타낼수 있다. 이때, 밑 첨자의 첫번째 글자는 면의 법방향, 두번째 글자는 stress의 방향을 의미한다. 즉$\sigma_{11}$는 normal stress이고 $\sigma_{12}$는 shear stress인 셈이다.
이번엔 $\sigma_{ij}=\sigma_{ji}$임을 증명해보자. 이 증명은 간단하다. 물체가 평형을 이루고 있으므로 물체의 미소 체적에 대해 FBD를 그리고 이에 대해서 $\sum M=0$을 계산하면 끝난다. 즉, 응력 텐서는 실대칭행렬이다. 이를 이용한 부가적인 내용은 추후에 stress transformation에서 다시 다룰 것이다. 지금은 stress가 텐서라는것 정도만 알아두자.
$\cdot$Strain(변형률)
외부에서 힘을 가하면 물체의 모양이 변형될 것이다. 이 변형된 정도를 나타내는 것이 바로 strain이다. Strain 역시 stress 처럼 Normal strain과 shear strain이 있다.
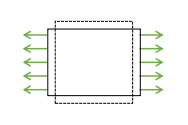
위 그림은 면에 수직한 방향으로 당겼을 때 나타나는 변형을 나타낸 것이다. 길이가 $L$인 물체가 늘어나 길이가 $L+\triangle L$이 되었을 때 normal strain은 $\varepsilon=\frac{\triangle L}{L}$으로 정의한다.
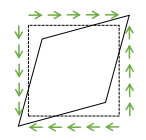
위 그림은 면에 나란한 방향으로 힘을 주는 pure shear stress에 의해 일어는 변형이다. 이때 shear strain은 아래와 같이 정의한다.
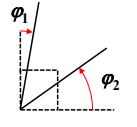
$$\gamma=\varphi_1+\varphi_2$$
위처럼 가장 기초적인 변형에 대해 알아보았으니, 이번에는 물체에 변형이 일어났을 떄 특정 지점에서 strain을 찾아보는 방법을 알아보자.
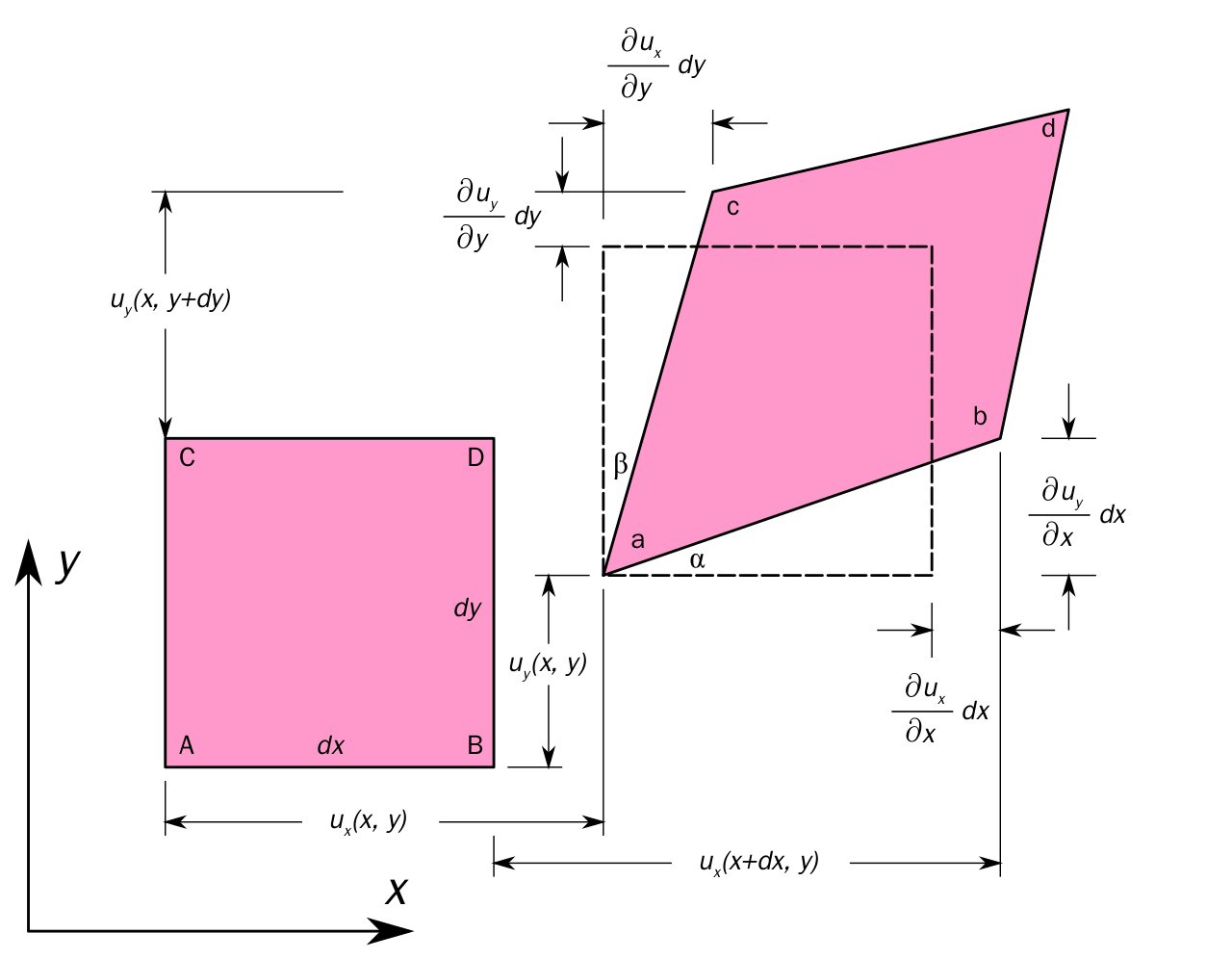
위의 그림에서 $u_x(x, y), u_y(x,y)$는 $(x, y)$지점에 있던 질점이 변형 후 $x, y$축 방향으로 얼마만큼 이동하였는가를 나타내는 변위에 대한 함수이다. 이떄 우리는 $[x, x+dx] \cap [y, y+dy]$의 아주 작은 직사각형 면적소에 대해 strain을 알아볼 것이다. $x, y$축 방향의 normal strain($\varepsilon_{xx}, \varepsilon_{yy}$)와 shear strain($\gamma_{xy}$)를 구해볼 것이다.
$$\varepsilon_{xx}=\frac{ab-AB}{AB}=\frac{\sqrt{dx^2((1+\frac{\partial u_x}{\partial x})^2+(\frac{\partial u_y}{\partial x})^2)}}{dx}-1=\sqrt{{(1+\frac{\partial u_x}{\partial x})^2+(\frac{\partial u_y}{\partial x})^2}}-1$$
$\varepsilon_{xx}$는 위와 같이 구할 수 있는데, 기본적으로 고체는 형태가 변하는 정도가 매우 작다. 즉, $\frac{\partial u_x}{\partial x}$와 같은 변위함수의 미분항들을 매우 작다고 하고 근사할 수 있는 것이다. 위 결과를 토대로 $\varepsilon_{xx}$를 다시 계산하면 아래와 같다.
$$\varepsilon_{xx}=\sqrt{{(1+\frac{\partial u_x}{\partial x})^2+(\frac{\partial u_y}{\partial x})^2}}-1 \approx \frac{\partial u_x}{\partial x}$$
마찬가지로, $\varepsilon_{yy}=\frac{\partial u_y}{\partial y}$이다. 마지막으로 shear stress의 경우는 아래와 같다.
$$\gamma_{xy} = \alpha + \beta \approx \tan \alpha + \tan \beta \approx \frac{\partial u_x}{\partial y} + \frac{\partial u_y}{\partial x}$$
위 결과를 토대로, 우리는 아래와 같은 일반화를 할 수 있다.
$\varepsilon_ij=\frac{1}{2}(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i})$, $x_1, x_2, x_3$는 각각 $x, y, z$에 대응
여기서 $\varepsilon_ij=\frac{1}{2}\gamma_ij$가 된다. 둘 다 shear strain을 나타내는 물리량이지만, 그 사용처가 약간 다르다. 먼저, $\varepsilon_ij$항의 경우 기본적으로 strain tensor를 나타내는데 쓰인다. strain tensor는 위의 stress tensor와 유사하게 정의된다.
$$\boldsymbol{\varepsilon} = \begin{pmatrix} \varepsilon_{11} & \varepsilon_{12} & \varepsilon_{13} \\\\ \varepsilon_{21} & \varepsilon_{22} & \varepsilon_{23} \\\\ \varepsilon_{31} & \varepsilon_{32} & \varepsilon_{33} \end{pmatrix}$$
Strain tensor를 정의하는 과정에서 shear strain을 나타내는 항에 $\frac{1}{2}$이 붙게 된 것이다. $\gamma$의 경우 이런것을 engineering formulation이라고 하는데, tensor를 도입하기 이전에 정의되어서 이렇게 두 가지의 shear strain을 나타내는 물리량이 생긴 것이다.
$\cdot$Thermal expansion
일반물리학을 공부하면서, 우리는 물체가 온도변화로 인해 길이가 아래와 같이 변할 수 있음을 배웠다.
$\frac{\triangle L}{L}=\alpha \triangle T$ ($\alpha$: Coefficient of thermal expansion)
이때, $\frac{\triangle L}{L}=\varepsilon$이므로 우리는 $\varepsilon_{thermal}=\alpha \triangle T$임을 알 수 있다. 그렇다면 물체가 외력에 의해 변형된 상태에서는 어떻게 될까? 해답은 아래와 같이 얻을 수 있다.
$$\varepsilon=\varepsilon_{mech}+\varepsilon_{thermal}=\frac{\sigma}{E}+\alpha \triangle T$$
총 변형률은 외부 load에 의한 변형과 열팽창에 의한 변형의 합이라고 놓고 strain, stress, temperature 사이의 관계식을 얻어서 해답을 얻을 수 있을 것이다.
$\cdot$Possion's ratio
일반적으로 우리가 지우개와 같은 물체를 잡아당길때, 길이는 늘어나고 두께는 수축하는 현상을 보았을 것이다. 이렇게 물체가 한 축 방향으로 늘어나면 나머지 축 방향에서도 길이 변화가 일어나게 된다.
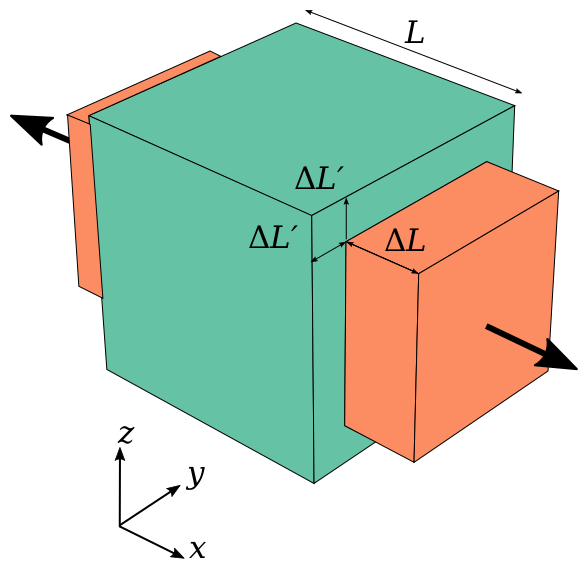
$$\varepsilon_{lateral}=-\nu\varepsilon_{axial}$$
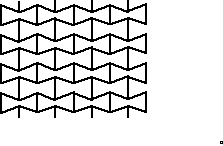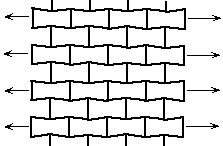
위의 식으로 한 쪽 방향으로 잡아당겼을 때 얼마만큼 다른 방향으로의 길이 변화가 일어나는지를 나타낼 수 있는데, 이 떄 상수 $\nu$를 Poission's ratio(푸아송 비)라고 한다. 일반적인 물체의 경우의는 양의 Poission's ratio를 가져 한쪽이 늘어나면 다른 방향은 수축하게 되는데, 아래의 그림과 같이 특수한 구조를 띈 경우 Poission's ratio가 음수가 되는 경우도 존재한다.
$\cdot$Relation of stress-strain
일반적인 우리가 마주항 isotropic한 물질들은, stress와 strain이 일정 범위 내에서 선형 관계를 만족한다.
$$\sigma=E\varepsilon , \tau=G\gamma$$
위의 선형 관계식에서 각각의 비례상수 $E, G$를 Young's modulus, shear modulus라고 한다. 이 두 물리량$(E, G)$는 재료의 특징을 나타내는 독립적인 matarials properties가 된다.
그런데, 우리는 앞에서 Poission's ratio를 알아보았다. 이 역시도 각 재료마다 가질 수 있는 고유의 특징이다. 그러나, 이 역시도 사실 $E, G$를 알 경우 아래의 수식을 이용해 구할 수 있다.
$$G=\frac{E}{2(1+\nu)}$$
즉, $(E, G)$뿐만 아니라 $(E, \nu)$ 역시 독립적인 materials properties가 될 수 있다. 위 공식에 대한 증명은 추후에 다시 다룰 예정이다.
이번엔, Poission's ratio를 활용하여, 1D에서가 아닌, 3D에서의 isotropic한 고체의 formula를 보도록 하자.
$$\varepsilon_{xx}=\frac{1}{E}[\sigma_{xx}-\nu(\sigma_{yy}+\sigma_{zz})]+\alpha \triangle T$$
$$\varepsilon_{yy}=\frac{1}{E}[\sigma_{yy}-\nu(\sigma_{xx}+\sigma_{zz})]+\alpha \triangle T$$
$$\varepsilon_{zz}=\frac{1}{E}[\sigma_{zz}-\nu(\sigma_{xx}+\sigma_{yy})]+\alpha \triangle T$$
$$\gamma_{xy}=\frac{\tau_{xy}}{G}, \gamma_{yz}=\frac{\tau_{yz}}{G}, \gamma_{xz}=\frac{\tau_{xz}}{G}$$
위의 공식을 글로 풀어서 생각해보면 단순하다. normal strain은 직접 당겨서 늘어난 것과, 옆면에서 당겨서 줄어든 것, 그리고 열팽창에 의한 것의 합과 같다는 것이다. 또한, shear 항과 normal 항이 서로 영향을 주지 않는다.
$\cdot$Yielding(Elastic vs Plastic)
위에서, stress와 strain은 "일정한 범위" 내에서 선형적인 관계를 만족한다고 하였다. 그렇다면, 그 일정한 범위라는 것은 무엇이고, 그 범위를 넘어가게 되면 어떻게 될것인지에 대해서 알아보자.
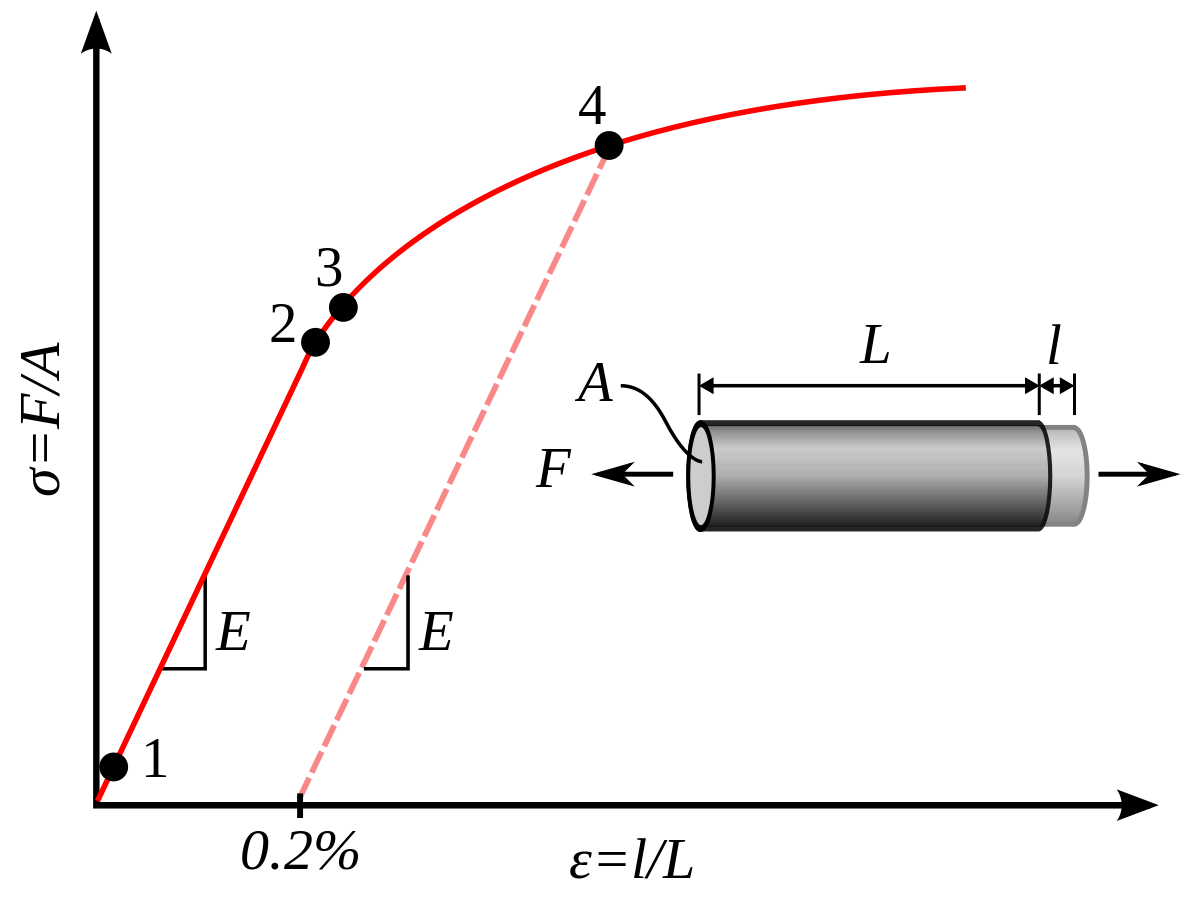
물체에 인장력을 가하여 잡아늘였다가 놓으면, 늘어났다가 줄어들게 된다. 이는 매우 직관적인 사실이다. 그러나, 일정 이상 힘을 가하면, 원래 상태로 돌아오지 않게 된다. 이 때, 우리는 영구적인 strain이 원래 길이의 0.2%의 상태로 돌아오도록 한 stress에 대해서 이를 yield stress(항복 응력)이라고 한다(4번 지점). Yield point까지의 범위를 elastic deformation(탄성 변형)이 일어났다고 하고, 그 뒤로는 plastic deformation(소성 변형)이 일어났다고 한다. Plastic deformation이 일어난 물체더라도, 힘을 unload할때는 elastic하게 변형되고, 또한 그 물체를 다시 잡아당길때도 plastic deformation을 일어나게 한 해당 stress에 도달하기 전까지는 똑같이 elastic하게 거동한다(위 그림의 점선 거동). 그 이유를 살펴보자.
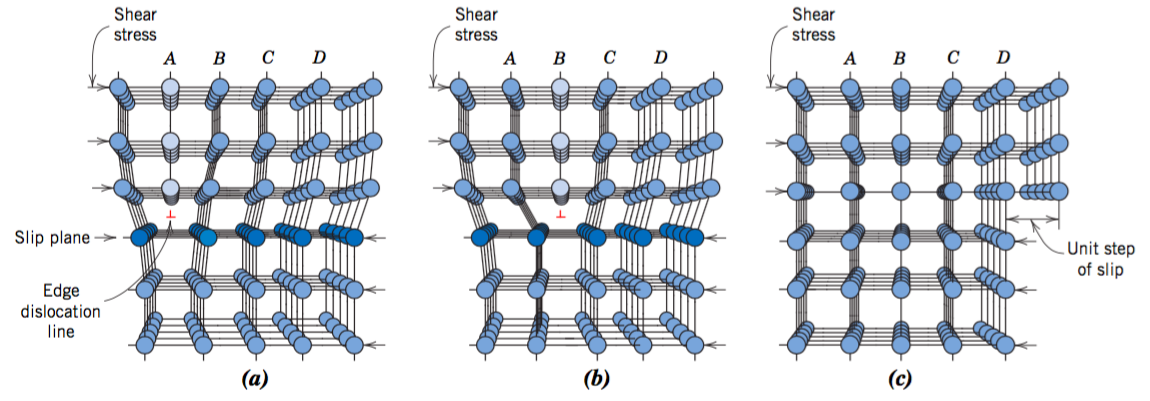
위 그림 (a)를 살펴보면, 고체의 격자 구조에 결함이 존재한다. 그런데 이 dislocation이 shear stress에 의해 그림 (b)처럼 밀리다가 변형이 한계치를 넘으면 그림 (c)처럼 영구적으로 그 구조가 변형된다. 이러한 구조의 미세한 결함때문에 plastic deformation이 생기는 것이다. 그렇기 때문에 plastic deformation이 일어난 이후에도 다시 elastic하게 거동할 수 있는 것이다. 그리고 plastic deformation이 일어나기 시작해도 $\sigma-\varepsilon$의 관계가 증가함수를 이루는 데, 이 이유가 dislocation이 정렬되기 때문이다.
고체의 $\sigma-\varepsilon$거동 그래프는 그 형태에 따라 여러갖지 이름이 붙어있는데, 우리는 여기서 시험문제에서 가장 흔히 볼 수 있는 이상적인 모델들을 보자.
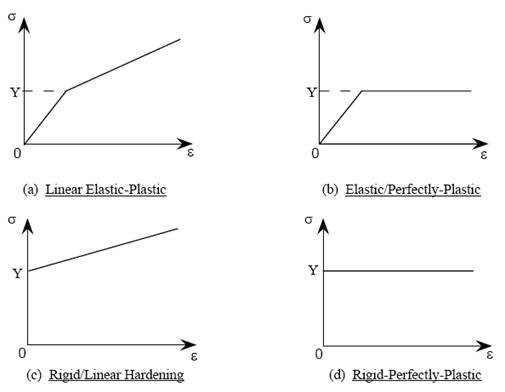
위의 그림들은 문제에 나올 수 있는 가장 기본적인 그림들이다. 일부 시험문제엔 Elastic-perfectly plastic한 물체다라고만 주고 stress-strain curve는 안 줄 가능성이 있으니 기본적인 것은 알아두는 것이 좋다.
$\cdot$Fatigue
고체에 지속적으로 아래 그림과 같은 stress를 가하면, fracture이 일어날 수 있다.
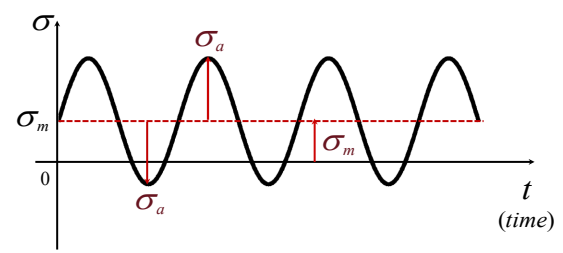
당연하게도, $\sigma_m, \sigma_a$의 값에 따라서 가능한 cycle의 반복 횟수 $N$도 변한다. 아래의 S-N curve와 Goodman diagram을 통해서 알아보자.
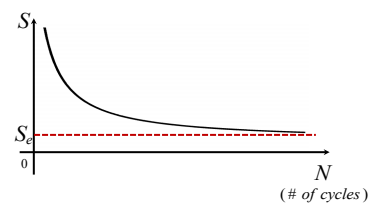
위의 S-N curve에서 $S=\sigma_a$를 의미한다. $\sigma_m$이 주어져있을 때, S와 N의 관계를 파악하여 주어진 amplitude에 대해 버틸 수 있는 cycle의 횟수를 알아낼 수 있는 것이다. 그리고 Stress amplitude가 일정 아래로 내려갈 때, 더 이상 cycle의 반복에 의해 fracture가 일어나지 않는 endurance limit가 존재한다.
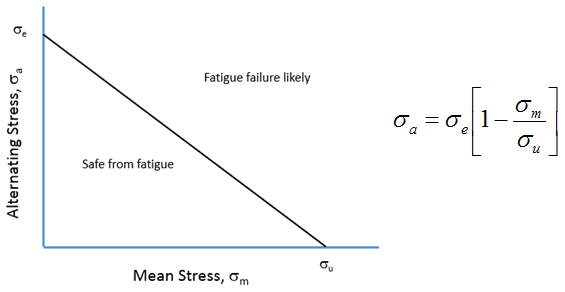
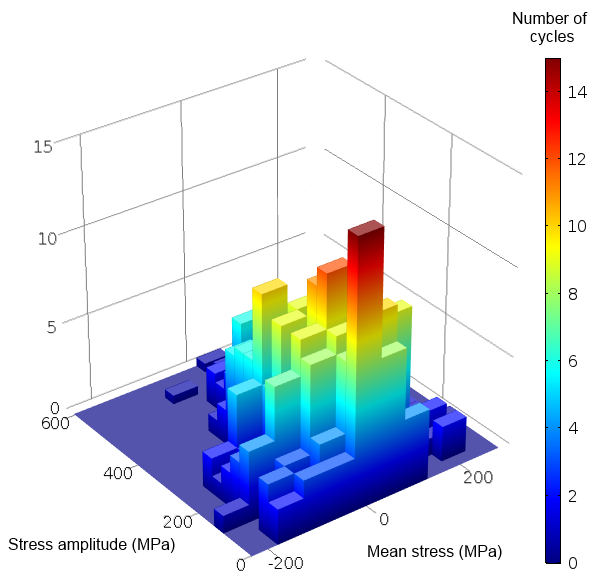
위 그림은 goodman diagram으로, 주어진 $N$값을 두고, $(\sigma_m, \sigma_a)$가 $N$번의 cycle이내에 fracture을 일으키는지 여부에 따라 allowable region과 failure occur region을 나타낸 것이다. $N$이 커질수록 위의 S-N curve에서 알 수 있듯이 $N$번의 cycle이후 fracture을 일으키는 $\sigma_a$가 작아질 것이다. Goodman diagram과 S-N curve를 종합하여 그린 3d plot은 아래와 같다.
$\cdot$Residual Stress
Residual stress는 system에 plastic deformation이 일어났을 때, 그 원인이 되었던 force를 unload해도 system 내에 남아있는 stress를 말한다. 대표적인 예시로 아래의 그림을 보자.

강철 막대를 구부려서 plastic deformation을 일으킨 뒤에도 여전히 물체 내부에 stress가 존재한다. 물론, 외력이 없으므로임의의 단면을 잘랐을 때의 force, moment는 0일 것이다. 그러나, 각 지점의 stress는 여전히 0이 아닌 상태로 있을 수 있다는 뜻이다. 위의 그림에서는 안쪽의 residual stress는 인장력, 바깥쪽의 residual stress는 압축력으로 존재할 것이라고 하는데 이는 왜 그런지 알아보자.
Residual stress를 구하는 방법은 의외로 간단하다. Residual stress의 개념이 외력이 unload될 때 생기는 것이고, 우리는 위에서 plastic deformation이 일어나더라고 unload될 때는 elastic하게 unload된다는 것을 알았다. 즉, 아래와 같이 식을 쓸 수 있다.
$$\sigma_{res}=\sigma_{load}+\sigma_{unload}$$
여기서 $\sigma_{load}$는 원래 상태에서 load를 가해 plastic deformation을 고려하여 구하고, $\sigma_{unload}$는 "원래 system의 상태"에서 아까와 정반대의 load를 가하면서 오직 "elastic"한 경우만을 고려하여 계산한다. 그 이유는, unloading을 원래 걸어놓은 load와 정반대의 load를 걸어 상쇄시키는 것으로 해석하고, 또한 unloading 과정에서는 elastic deformation만이 일어나기 때문이다. 이를 토대로 위의 그림에서 왜 residual stress가 아래쪽이 tension, 위쪽이 compression인지 알아보자.
이에 앞서, beam의 deformation은 아직 다루지 않은 내용이다. 그렇기에 여기서는 문제를 풀기 위한 아주 기본적인 정보만을 제공할 것이다.
$\cdot$Beam의 strain 및 stress는 기본적으로 길이방향과 나란한 성분이다.
$\cdot$Beam의 strain은 중심축(Neutral axis)와의 거리에 비례한다. $\varepsilon_{xx}=-\kappa y$ (tensile이 양의 값)
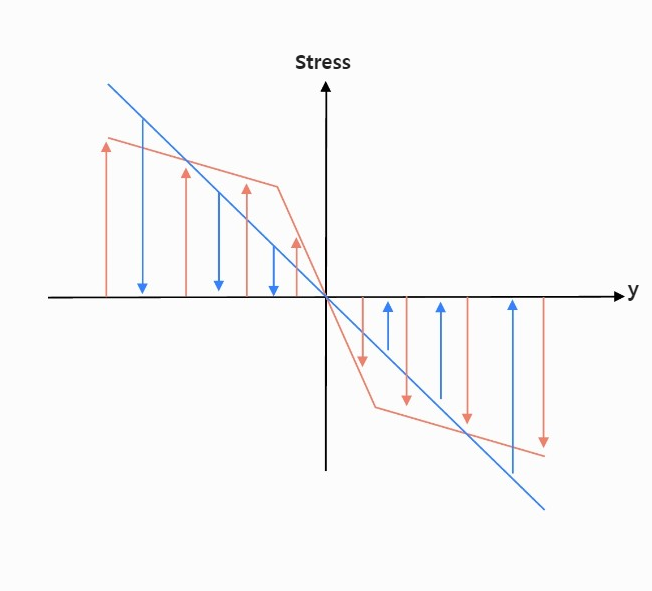
Plastic deformation을 고려한 loading의 경우, strain이 yield point를 넘어가는 순간부터 plastic deformation이 시작되었을 것이다. 그리고 unloading의 경우는 elastic한 상황만을 고려하므로 직선이 그려질 것이다. 이때, elastic할 때도 두 직선의 기울기가 다른 이유는 간단하다. $\varepsilon_{xx}=-\kappa y$에서 $\kappa$값이 다르기 때문이다. 여기서 $\kappa$는 beam의 휜 정도를 나타내는 곡률인데, plastic변형이 일어날 때와 일어나지 않을 때의 변형이 동일할 수가 없다. 그리고, $\sigma_{load}, \sigma_{unload}$의 대소관계가 바뀌는 이유는 둘 다 동일한 크기의 moment에 의해 일어난 변형이므로 $M=\int \sigma y \ dA$의 크기가 같게 나타나야하기 때문이다. 위의 결과를 통하여 residual stress를 구하면 아래와 같다.
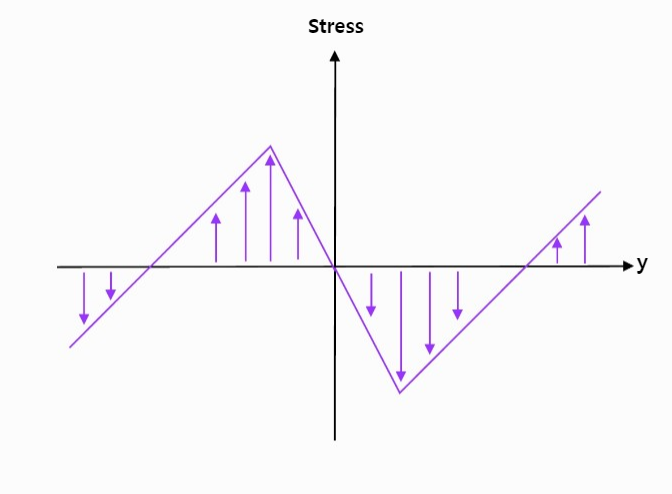
이 그림을 통해, 우리는 beam이 휘면서 compression을 받았던 부분의 residual stress는 tensile이고, tensile이 작용되었던 부분의 residual stress는 compression임을 알 수 있다.
'기계공학 > 고체역학' 카테고리의 다른 글
| 1. Statics (0) | 2022.07.22 |
|---|
