1. Statics

 정역학(Statics)은 정적 평형 상태에 있는  계(system)을 보는 학문이다. 흔히 자주 볼 수 있는 역학적인 평형상태에서 문제를 푸는 것이다.

 그렇다면 어떠한 것을 푸는지 알아보자. 정역학이라고 한 것에서 이미 계는 평형을 이루고 있다. 그 계가 평형을 이루게 하기 위해서는 어느 지점에 어느 정도의 힘이 가해지고 있는지 알아내는 것, 그것이 정역학이다.

 앞서 말했듯 정역학의 기본은 평형을 이루고 있는 상태, 즉 $\sum F=0$이다. 그런데 이것만으로는 물체의 병진운동을 설명할 수 는 있어도 물체의 회전운동을 설명할 수 는 없다. 이를 위해서 모멘트(Moment, 고체역학에서는 돌림힘 혹은 토크라고 하는 것이 더 익숙할 수도 있다.)라는 개념을 가져올 것이다.

 

$\cdot$Moment

 모멘트는 다음과 같이 정의된다.

$$M=r \times F$$

 이는 물체가 해당 회전축을 기준으로 회전시키려는 효력을 의미하는 물리량이다. 정역학에서는 알짜 모멘트의 값이 0이 되어야 하므로, 계의 모든 곳에서 $\sum M=\sum r \times F=0$을 항상 만족하여야 한다.

 

 모멘트 중에서 $r \rightarrow 0$인 점 모멘트(Point Moment)는 문제를 풀 때 꽤 자주 등장하는 요인이다. 그런데 모멘트는 $r$이 0이 되면 0이 될 수 밖에 없는데, 점 모멘트는 대체 무엇일까? 이는 보통, 축(shaft)를 통해 전달되는 모멘트를 말하거나, 크기가 작은 요소에서 발생하는 돌림힘에 대한 근사이다. 

 

 

 

$\cdot$Free Body Diagram(FBD)

 FBD는 계에서 내가 필요로 하는 물체를 지정해서, 그 물체에 작용하는 모든 힘과 모멘트를 표시한 것을 말한다. 이때, 지정한 subsystem의 경계에 닿아있는 다른 요소들 역시 그리지 않고 오직 외부에 의한 힘과 모멘트를 표시해야한다. 예를 들어, 실에 걸린 물체에 대해 FBD를 그릴 때 장력을 표시할 뿐 실은 그리지 않는 것이다. FBD의 대표적인 예시로, 마찰이 있는 빗면 위에 멈춰있는 물체에 대해 아래와 같이 그릴 수 있다.

 

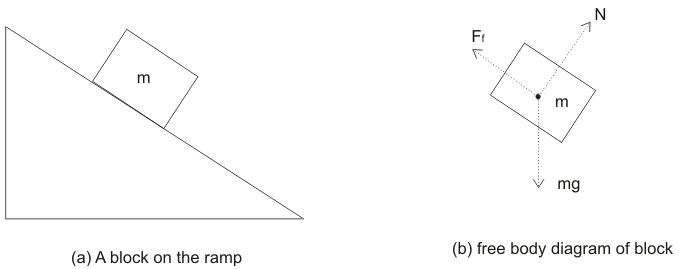
-Two Force system

 정역학 문제에서는 일자형 막대를 포함하는 system이 매우 자주 나온다. 즉, 우리는 여기서 막대에 대한 정역학적 해석을 하고 넘어가야 할 것이다.

 트러스 구조와 같은 형태에서 보통 막대는 양 끝 지점에서만 힘을 받는다. 이처럼 두 지점에서만 힘을 받는 system을 two force system이라고 하는데, 이 때 이 막대에 대해 FBD를 그래서 평형 조건을 살펴보면, 다음 조건을 만족한다.

1. $F_1=-F_2$, 즉 힘의 크기가 같고 방향이 정반대이다.                          

2. 두 힘이 colinear, 힘의 방향과 두 작용점을 잇는 선분이 나란해야 한다.

 우리는 이미 일반물리학에서 위 조건을 자주 썼었는데, 장력이 걸린 실에서 장력이 실에 나란하게 걸리는 것이 바로 실이 two force system이기 때문이다. 즉, two force system에서는 힘을 두 작용점을 이은 선분과 나란하게 그려주면 된다.

 

 

-Mechanical action at support

 정역학 문제에서는 보통 system을 지지하는 support들이 있는데, 이들은 종류에 따라서 다양한 reaction force, moment를 가하며 계가 평형상태에 있도록 한다. Support들의 종류는 대표적으로 아래와 같다.

 위의 표는 각각의 support들의 reaction을 나타낸 것이다. 해당 support들은 고체역학을 공부하는 동안 계속해서 나오는 사항이니 알아두어야 한다.

 

 

$\cdot$Solve statics problem

 FBD를 그릴 subsystem의 설정이 복잡한 정역학 문제를 푸는 것에 있어서 매우 중요하다. 특히, 트러스 구조와 같이 계를 구성하는 구성요소가 매우 많을 때 더욱 그렇다. 이제부터, 아래의 예시 문제를 풀어보면서 정역학 문제를 푸는 감각을 익히도록 하자. (본 글에서는 기본적인 풀이 과정만 설명하고 계산은 생략한다.)

1) 먼저, 전체 system에 대해서 FBD를 그려서 힘을 분석해본다. 이때 A는 pin, E는 roller이므로 A에 작용하는 Reaction force는 $R_{Ax}, R_{Ay}$가 있고,  E에 작용하는 Reaction force는 $R_{Ey}$가 있다.

 이 세 미지수에 대하여 $\sum F_x=0, \sum F_y=0, \sum M=0$을 풀어주면 아래와 같은 해를 얻을 수 있다. 

$$R_{Ax}=0, R_{Ay}=35N, R_{Ey}=25N$$

 

 BH member에 가해지는 힘을 찾기 위해서는, 각각의 joint들이 역학적 평형상태를 띄고 있어야 하는 것을 이용한다. 위 그림에서 각각의 member들은 전부 two force system인 것을 활용하여, 각 member가 받는 힘들의 방향을 정할 수 있다. 이때, 각각의 힘들을 막대 안쪽으로 향하게 하느냐 바깥으로 향하게 하느냐는 문제를 푸는 사람의 마음에 달렸다. 그렇지만, 실수를 줄이기 위해 방향성을 전부 통일해주는 것이 좋다. 실제로 이 힘이 인장력인지 압축력인지는 구한 힘 크기의 부호를 보고 판단하면 된다. 이 문제에서는 전부 압축력을 +으로 두었다.

 

2) 점 A에서 $\sum F=0$을 이용하여 $F_{AG}, F_{AB}$를 구할 수 있다. 값은 아래와 같다.

$$F_{AB}=-35N, F_{AG}=49.5N$$

 

3) 위와 같이 점 G에서도 같은 방법으로 풀어주면, $F_{BG}=-35N, F_{GH}=35N$을 얻는다.

 

4) 마지막으로, 점 B에서 이 방법을 적용하면, $F_{BH}=21.1N$을 얻는다. 즉, member BH는 compression을 받는다는 것도 확인할 수 있다.

 

 

다른 예시 문제로, 막대가 two force system이 아닌 경우에 대해서 풀어보자.

 

 위 문제 같은 경우에는, member ABC와 member CDE에서 $F_{BD}$의 존재로 인해 two force system이 아님을 확인할 수 있다. 즉, 아까처럼 힘을 member의 방향과 나란하게 둘 수 없는것이다. 이럴 때는, joint에서 member에 가하는 힘을 각각 $F_x, F_y$로 두고 풀어야 한다.

 

1) 전체 system에서 FBD를 그려서 풀어보면, $-R_{Ax}=R_{Ay}=R_{Ex}=196.2N$임을 알 수 있다.

 

2) member CDE와 ABC에서 FBD를 그려본다. 이 때, 점 C에서 힘을 표현하는 것이 골칫거리일 것이다. 이를 위해, 질량 $m$이 member ABC, CDE중 한 곳에 매달려 있다고 가정하자. 그리고 joint에서 힘이 평형을 이루어야 하므로 두 member가 받는 reaction force는 크기가 같고 방향이 반대가 되도록 그려야 함에 유의하자. 정상적으로 문제를 풀면, 아래와 같은 결과를 추가로 얻는다.

$$R_{Cx}=196.2N, R_{Cy}=F_{BD}=392.4N$$

 

 마지막으로, 물체의 internal loading을 FBD를 통해 구해보자. Rigid body가 역학적 평형을 이루기 위해서는 internal loading을 통해 힘을 전달해 주어야 외력을 가해도 형태가 변하지 않을 수 있는 것이다.

 아래의 그림에서 점 C에서의 internal loading을 구해보자.

 표시한 점 C에서의 internal loading을 구하기 위해서 BC에 해당하는 부분을 잘라서 FBD를 그릴 것이다.

 

 선형 force density는 삼각형의 무게중심과 같이 고려할 수 있다. (이는 적분의 결과이다.) Figure (b)처럼 FBD를 그리고 평형 조건을 계산하면 아래 결과를 얻는다.

$$N_C=0, V_C=540N, M_C=-1080N \cdot m$$

 

 

 

 

 

 

$\cdot$Statically Determinate System(SDS) / Statically Indeterminate System(SIS)

 정역학적 계를 논할 때, 항상 이것이 SDS인지 SIS인지를 따져보아야 한다.

 먼저 SDS란, 아까 우리가 풀었던 문제들과 같이 완전한 강체로 가정하고 정역학적 평형 방정식만을 이용해서 풀 수 있는 system을 의미한다. 반대로 SIS는 위의 방법만으로는 모든 reaction을 구해낼 수 없는 system이다. 이 두 system의 가장 큰 차이는, unknown의 개수이다. 만들어낼 수 있는 방정식의 개수에 비해, 미지수들이 너무 많아서 모든 reaction을 구할 수 없는 것이다. 아래 예시를 보면서, 두 system의 차이를 보자.

 

 왼쪽의 그림에서 점 A에서의 reaction을 구하는 것은 그리 어렵지 않다.

$R_{Ax}=0, R_{Ay}=P, M_A=PL$임을 쉽게 찾을 수 있을 것이다. 이런 system들이 SDS인 것이다.

 

 

 

 

 그렇다면 이번엔 점 점 A와 B에서의 reaction을 동시에 구해보자. 그러나 이번에는 방정식은 $\sum F_x=0, \sum F_y=0, \sum M=0$으로 3개이지만, 미지수의 경우 $R_{Ax}, R_{Ay}, M_A, R_{By}$로 4개이다. 즉, 지금까지의 방법으로는 모든 reaction을 구할 수 없다. 이러한 system들이 SIS인 것이다.

 

 

 

 이러한 SIS의 경우, 물체의 변형을 고려하여 풀게된다. 우리가 흔히 강체라고 하는 것들도, 완벽하게 딱딱한 것이 아니다. 힘을 가하면 아주 조금이나마 힘에 따른 변형이 일어나게 되고, 그 작은 변형을 이용하여 추가적인 방정식을 이끌어내어 SIS의 reaction들을 구할 수 있을 것이다. 이는 추후에 다시 다루게 될 것이다.