다른 글 보러가기
2. 텐서로의 한 걸음, 좌표계
저번 글에서는 벡터라는 녀석을 조금 자세히 살펴보고, 각도와 길이에 대해 조금 깊은 얘기를 해봤습니다. 이제, 이 벡터라는 녀석을 이용해 공간을 표현하는 방법에 대해 생각해볼 차례입니다. 이번에는 좌표라는, 꽤 중요한 개념에 대해 다뤄보도록 합시다.
좌표계가 무엇일까요?
물리의 관점에서 한번 살펴봅시다. 일단 직교좌표계만 생각해봐도, 우리에게 직교좌표계라는 것은 꽤나 익숙하고, 어쩌면 당연해 보일 수도 있지만, 사실 데카르트가 이걸 만든 것은 당시 꽤나 혁명적인 일이었습니다. 숫자라는 것 부터 우리 머리속에 있는 추상적인 개념인데, 좌표라는 것은 실제 세계를 우리의 추상적인 세계로 가져오는 일입니다.
예를 들어봅시다. 저기 하늘 위에 예쁜 별이 떠있습니다. 저 별의 위치를 표현해볼까요?

"제가 보는 방향에... 손을 이정도 각도로 들면 가리킬 수 있어요!"
'제가 보는 방향' 이라니.. 어이가 없을 수 있겠지만, 이 정도면 별을 보는 나의 기준에서는 꽤 충분할 것 같습니다. 예를 들어, 지금 저 별이 보이는 방향을 기억해두고, 다른 별을 가리켜봅시다.

"몸을 이만큼 돌리면 손을 이정도 들어서 저 별을 가리킬 수 있는거죠!"
그런데, 이런 방식을 이용하면 하늘 위의 어떤 점이든 가리킬 수 있습니다. 처음 바라봤던 방향으로부터 몸을 돌린 정도와, 손을 들은 정도를 수치화하면, 숫자 두개로 하늘 위의 어떤 점이든 가리킬 수 있다는 것입니다. 이리 보면 의미 없는 논의같은데, 조금은 더 구체적으로 살펴봅시다.
하늘 위에 있는 것들은 얼마나 멀리 떨어져있는지 알기 어렵습니다. 그러니까, 우리 눈은 대충 하늘을 내 머리 위에 있는 돔 정도로 이해할 것입니다. 다음 그림을 봅시다!

그리고, 이 돔 위의 점은 기준(빨간 선)으로부터 몸을 돌린 정도

평면 위의 점을 표현하는 극좌표계, 공간 상의 점을 표시하는 구면좌표계와 원통좌표계, 또한 이들과 직교좌표계의 변환까지도 열심히 공부했을 것입니다. 극좌표는
평면 위에 다음과 같은 격자를 두고 생각해봅시다.
이 격자 위에 적당한 점 O를 잡고.. 저번처럼 격자 간의 이동의 기저를 잡아봅시다.
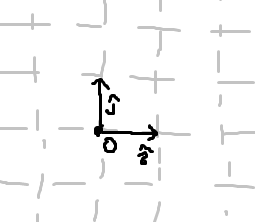
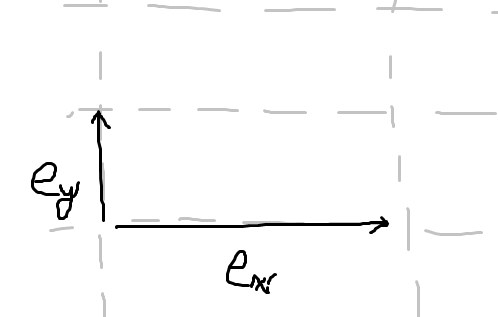
이제, 점 O로부터 어떤 점 P로의 이동이
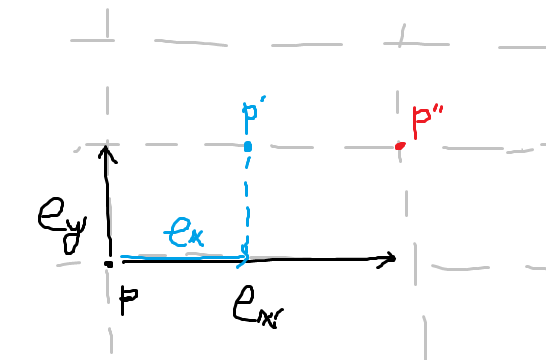
이제 생각해 볼 것은 조금 다른 것입니다. 예를 들어, 어떤 점
그렇다면, 이 변화 후 나타나는 점
애초에 벡터로 점을 표시하고 있었으니,
사실,
라고 쓰는 것도 큰 무리는 아닙니다. 즉, 다음과 같이 식을 고쳐써봅시다.
결국, 점
이번에는 조금 다른 격자를 들고 와 봤습니다.
그렇다면, 마찬가지로 어떤
위와 같은 논리로, 점
이제 점
그렇다면, 점
임을 알 수 있습니다.
그런데,
이를 보면, 기저 벡터에 해당하는
좌표계 변환에 대해 조금 더 생각해봅시다!
선형대수학에서 배우기를, 기저벡터의 변화는 가역행렬을 통해 표현 가능합니다.
예를 들어서,
라 표현 가능하고, 다음과 같은 조금은 무례한 표현을 사용할 수도 있습니다. (뭐가 문제일까요? 하하)
이제,
일단, 밑첨자는 행, 윗첨자는 열로 이해해봅시다. 그러면 다음과 같이 쓸 수 있습니다.
같은 방식으로, 반대 방향으로도 생각해볼 수 있습니다.
표기법의 오용이 조금 있다고 생각될 수 있지만,
이러한
(왜 크로네커 델타가 저렇게 위아래로 써졌는지는 언젠가 알아봅시다. 일단 기존의 정의대로,
그렇다면, 이제 어떤 벡터가 다음과 같이 표현된다고 해 봅시다.
그리고, 또다른 기저에 대해,
처럼 표현된다고 해 봅시다.
그런데, 이 둘이 같은 벡터를 나타내는 것을 확인하기 위해서, 좌표계 변환을 도입해봅시다.
즉, 다음과 같은 두 식이 나옵니다.
뭔가 보이나요? 아직 보이기 쉽지 않으니, 지금까지 한 걸 다 모아 다음과 같은 표기를 써 봅시다.
이제 뭔가 좀 보이는 것 같지 않나요? 프라임이 위에 붙은것과 아래 붙은것은 서로 역행렬관계라고 했는데, 기저를 변환시키는 좌표계 변환이 기저 앞에 붙는 성분에는 역으로 작용합니다.
다시 말해 기저의 변환과 성분의 변환은 반대의 관계에 있습니다. 이러한 의미로 성분은 기저 변환에 대해 반변이라 말합니다. 우리는 반변하는 것에 대해 윗첨자로 쓰기로 합니다. 이렇게 하면 위의 시그마로 표현한 두 식이 단순히 약분처럼 보일 것입니다. 애초에 우리는 이 벡터가 불변인 것에서 시작했습니다.
기저의 좌표 변환에 대해 그 성분이 이와 같은 변환이 잘 이루어지는 것을 (물리학에서) 벡터라 부릅니다.
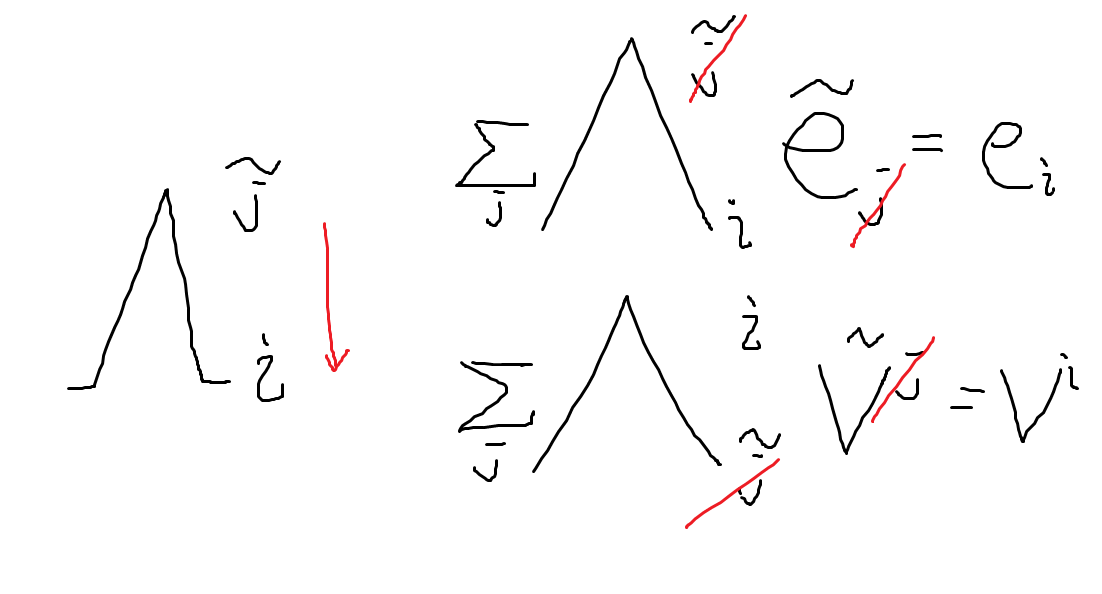
그런데, 이런 이동으로 표현할 수 있는 좋은 좌표계가 있는 반면, 그렇지 못한 좌표계가 존재합니다.
바로 위에서 논의했던 휘어져 있는 좌표계 들이죠.
이를 논하기 전에, 지금까지 논한 좋은 좌표계들의 성질을 봅시다. (이동으로 표현한)
점
그렇다면, 이 미소 변화 후의 점
으로 표현할 수 있습니다.
미소 이동은 휘어진 좌표계에서도 비슷하게 논의해볼 수 있을 것 같습니다. 2차원에서 가장 친숙한 친구, 극좌표계를 가져와봅시다. 어떤 점이
첫 번째.
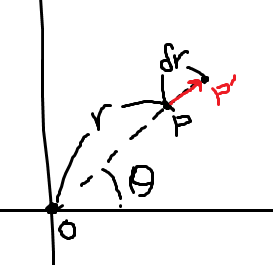
즉,
을 만족하는
두 번째.
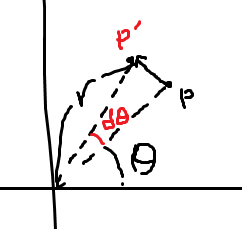
똑같이
가 되도록 하는
즉, 이제 어떤 점
애매하다고 생각할 수 있지만, 간단하게 다른 좌표를 모두 고정하고 하나의 좌표만 움직이면 생기는 곡선의 속도가 이 기저벡터입니다. 아래 그림을 봅시다.
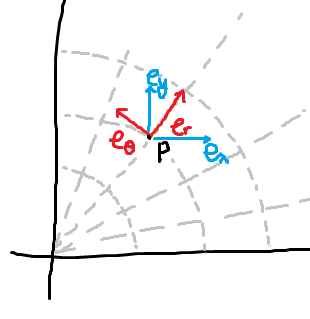
아무튼 국소적으로는 휘어진 좌표계도 위에서 논의한 것과 같은 논의를 해볼 수 있습니다. 벡터가 생겼으니까요!
즉, 어떤 점
그런데, 이
다음 편에는 인간이 휘어진 것을 이해하는 방법, 미분에 대해 고찰해보도록 합시다.
'물리학 > 물리수학' 카테고리의 다른 글
| [텐서론 기초] 1. 당신, 벡터는 잘 알고 있나요? (2) | 2023.03.13 |
|---|---|
| [텐서론 기초] 0. 그래서 텐서가 뭔가요? (0) | 2023.03.10 |
![[텐서론 기초] 2. 텐서로의 한 걸음, 좌표계](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FcTqbyn%2Fbtr4guRwYrd%2FylGSKJg0YKYFLbtUaROgGk%2Fimg.png)