[텐서론 기초] 1. 당신, 벡터는 잘 알고 있나요?

저번 글 보러가기

0. 그래서 텐서가 뭔가요?

1. 당신, 벡터는 잘 알고 있나요?

2. 텐서로의 한 걸음, 좌표계

 

텐서라는걸 알기까지는 꽤 먼 길을 달려가야 할 필요가 있습니다. 물론 이름도 멋지고 바로 알 수 있다면 참 좋겠지만, 우리 한번 지금까지 걸어온 길을 돌아봅시다. 일단 간단한 질문부터 던져보고자 합니다. 벡터가 뭘까요?

 

여기에 다양한 대답이 나올 수 있겠지만 우리 한번 어디서 접해봤는지 쭉 살펴봅시다.

먼저, 고등학교의 기하라는 과목에서 접해봤을 수 있습니다.

(물론 저는 기하와 벡터에서 접했습니다. 이 글을 지금 읽고 있을 정도면 아직은 기하에서 벡터를 접한 사람보단 기하와 벡터에서 벡터를 접했던 사람이 많겠죠..? 그렇길 바라고 있습니다.)

"벡터는 크기와 방향을 가진 양이에요!"

 

고등학교에서 배우는 벡터는 일종의 화살표 입니다.

이걸 더하고.. 늘리고... 온갖 짓을 다했죠.

이걸 언제 쓰나 했더니 대학교에 입학하자 마자 바로 등장합니다.

 

"으으..."

 

미적분학이라는 과목에서는 이 벡터를 가지고 미분을 하고.. 미분을 했더니 벡터가 나오고 별 난리를 다 칩니다. 공부하다 보면 미적분과 벡터를 동시에 배우지 않고 이걸 공부하는게 말이 되나 하는 고민이 드는 내용을 배우곤 합니다.

 

그렇지만 여기까지는 그래도 고등학교때 배운 벡터랑 크게 다를 게 없어 보입니다.

그런데 저기 있는 다른 친구가 의견이 있나 봅니다.

 

"뭔 소리야, 벡터는 벡터 공간의 원소지"

 

그렇습니다. 선형대수학에서 배우는 벡터는 덧셈과 상수곱이 주어져있는 벡터 공간의 원소입니다. 

여기 잘 설명해둔 글도 있으니 한 번 상기하고 오는 것도 좋겠네요!

 

그럼 이제 의문이 생깁니다. 대체 뭐가 맞는걸까요? 사실, 무엇도 틀린 것은 없습니다. 그저 조금 다른 것을 얘기하고 있을 뿐이죠. 이제 우리는 고등학교때 배운 크기와 방향을 가진 양에 선형대수학 한 스푼을 첨가해줄 필요가 있습니다. 그것이 물리학에서 말하는 벡터가 되리라 생각이 드네요!

 

일단 고등학교에서 배우는 벡터를 살펴봅시다.

이 때 배우는 벡터는 일종의 두 점 사이의 (직선)이동입니다.

이 이동에도 상수배와 덧셈이라는 연산을 줘볼 수 있습니다.

 

상수배라는 연산은 배율로 이동 거리를 늘리고 줄이거나, 음수를 곱하여 뒤집는 행동이고,

덧셈이라는 연산은 어떤 이동 뒤에 다른 이동을 이어붙이는 행동을 의미합니다.

 

그런데 이 이동이라는 행동은 직선 이동이기 때문에, 평행사변형의 성질이나 닮음의 성질을 잘 조물조물하여 우리가 준 이 연산 아래에서 이동은 벡터가 됨을 어렵지 않게 생각할 수 있습니다.

Exercise. 가만히 있는 이동 (이를테면, 점 A에서 점 A로 이동하는 행위)을 이동에 포함했을 때, '이동'의 집합이 벡터공간이 됨을 보여봅시다!

선형대수학에서 배우는 것 중 하나는 어떤 (유한 차원) 벡터든, 기저 를 잘 잡아 다음과 같은 좌표계 표현이 가능하다는 것입니다. 즉, 임의의 (실수)벡터공간은 $\mathbb{R}^d$와 isomorphic합니다! (우리의 철학, 같은 것은 같다.)

$$[v]_\beta = \pmatrix{a\\b}$$

그렇다면, 우리는 어떤 기저를 잡아야 위와 같은 표현을 할 수 있을까요? 어렵지 않습니다. 우리의 마음 속에는 언제나 직각 격자가 있기 때문에, 그 마음 속에 있는 격자를 꺼내오면 될 것 같습니다.

'마음 속의 격자'

이 우리의 격자 에서 오른쪽으로 한 칸 움직이는 이동을 $\hat{i}$라 하고, 위로 한 칸 움직이는 이동을 $\hat{j}$라 하면, 위 그림에 보이는 세 개의 이동을 이 격자 이동을 통해 표현해볼 수 있습니다. 

$$\overrightarrow{\rm{AB}}=2\hat{i}+\hat{j}$$

$$\overrightarrow{\rm{BC}}=-\hat{i}+\hat{j}$$

$$\overrightarrow{\rm{AC}}=\overrightarrow{\rm{AB}}+\overrightarrow{\rm{BC}}=\hat{i}+2\hat{j}$$

좋습니다. 그렇다면 우리는 $\overrightarrow{\rm{AC}}$ 같은 벡터를 $[1,2]$ 같은 순서쌍으로 나타낼 수 있을 것 같은 자신감이 듭니다. 예를 들어, 지금 점 $\rm{A}$의 위치가 원점이라면, 점 $\rm{B}$의 좌표는 $(2,1)$일테고, 이는 원점에서 점 $\rm{B}$로의 이동과 동일하게 나타납니다. 이런 것을 기하와 벡터에서는 위치벡터라고 표현했었지요.

 

그렇지만, 이동을 단순히 순서쌍으로 나타내는 것은 조금 문제가 있을지도 모릅니다. 누군가 마음이 삐뚤어져 다음과 같은 격자를 마음속에 품고 있다고 해 봅시다.

새로운 격자 위에서는 세 점 사이의 이동은 다음과 같이 표현될 것입니다.

$$\overrightarrow{\rm{AB}}=\hat{i}^\prime$$

$$\overrightarrow{\rm{BC}}=\hat{j}^\prime$$

$$\overrightarrow{\rm{AC}}=\overrightarrow{\rm{AB}}+\overrightarrow{\rm{BC}}=\hat{i}^\prime+\hat{j}^\prime$$

이번에는 그럼 $\overrightarrow{\rm{AC}}$ 라는 벡터는 $[1,1]$ 이라는 순서쌍으로 나타나게 될 것입니다. 

 

결국, 처음 격자의 기저 $\beta=\left\{\hat{i}, \hat{j}\right\}$과 삐뚤어진 격자에서의 기저 $\beta^\prime=\left\{\hat{i}^\prime, \hat{j}^\prime\right\}$를 통해 $\vec{v}=\overrightarrow{\rm{AC}}$라는 이동을 다음과 같이 쓸 수 있습니다.

$$[\vec{v}]_\beta = \pmatrix{1\\2}$$

$$[\vec{v}]_{\beta^\prime} = \pmatrix{1\\1}$$

결국 두 표현은 같은 벡터를 나타내는데, 이 둘이 같은 것을 나타내는 것을 알 방법이 있을까요?

 

다시 처음으로 돌아가봅시다. 우리는 고등학교에서 배우는 벡터에 대해 생각해보고 있었고, 이것은 크기와 방향을 가진 대상이었습니다. 사실 우리는 이에 대해 여태껏 단 한 번도 논하지 않았습니다. 

 

분명히 두 결과 $[1,2]$, $[1,1]$는 같은 것인데 표현이 다릅니다. 이 둘이 다른 것은 기저이니, 기저가 이동의 크기와 방향을 품고 있는 것이다.라는 추측을 감히 해볼 수 있습니다.

 

이제, 이동의 크기를 다음과 같이 간단히 정의해도 큰 문제가 없을 것 같습니다.

어떤 이동 $\vec{v}$가 주어져 있을 때,  $\vec{v}$의 시작점과 도착점 사이의 거리를 이  $\vec{v}$의 크기라 부르고,  $||\vec{v}||$와 같이 표현한다.

중학교때부터 아주 익숙한 피타고라스 정리를 이용하면, 이동의 크기는 아주 간단하게 구할 수 있습니다.

$$|\vec{v}|^2=1^2+2^2=5$$

사실, 직각 격자로 표현한 이동은 그 표현만으로 아주 쉽게 크기를 구할 수 있습니다.

$$[\vec{v}]_\beta = \pmatrix{a\\b}$$

$$|\vec{v}|=\sqrt{a^2+b^2}$$

그렇다면, 위에서 논의한 삐뚤어진 격자, 즉, $\beta^\prime$으로 표현한 이동의 크기는 어떻게 구할 수 있을까요?

벡터의 크기?

죠$\hat{i}^\prime$과 $\hat{j}^\prime$ 사이의 각도 $\theta$가 주어져 있다면, 코사인 법칙을 통해 이 크기를 구해볼 수 있을 것 같습니다. 그렇다면, 다음과 같은 벡터의 크기가 똑같이 $\sqrt{5}$ 가 나와야 할 것입니다.

$$[\vec{v}]_{\beta^\prime} = \pmatrix{1\\1}$$

사실, 우리는 두 기저 $\hat{i}^\prime$과 $\hat{j}^\prime$의 크기도 각각 알고 있습니다. $\sqrt{2}$와 $\sqrt{5}$일 것입니다. 이를 이용해 $\vec{v}$의 크기를 구하는 식을 세워봅시다.

$$|\vec{v}|^2=2+5+2\sqrt{10}\cos\theta=5$$

이제, $\cos\theta$의 값을 바로 구할 수 있으니, 임의의 $\beta^\prime$-표현으로 나타난 이동의 크기가 다음과 같이 나타남을 알 수 있는 것입니다.

$$[\vec{v}]_{\beta^\prime} = \pmatrix{a\\b}$$

$$|\vec{v}|^2=2a^2+5b^2-2ab$$

크기는 잘 구했습니다. 이제 우리는 $\beta$-크기와 $\beta^\prime$-크기를 알고 있다 라고 생각할 수 있을 것 같습니다. 이제 방향에 대해서 조금 생각해볼 차례입니다. 

 

물론, 이 '방향'도 고등학교 기하에서 충분히 다루는 내용입니다. 다음과 같은 내적이라는 연산이 있습니다.

두 이동 $\vec{v}$와 $\vec{w}$, 그리고 그 둘이 이루는 사이각 $\theta$에 대해,
$$\vec{v}\cdot\vec{w}=|\vec{v}||\vec{w}|\cos\theta$$ 를 두 이동 $\vec{v}$와 $\vec{w}$의 내적이라 부른다.

내적

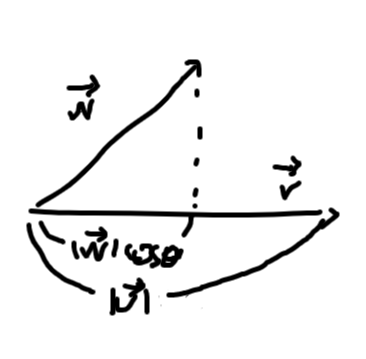
즉, 이 내적이라는 것은 이동 사이의 각도를 알려줍니다. 그렇지만, 실질적으로 구하기 어려울 것 같기도 합니다. 애초에 두 이동이 이루는 각도를 알아야 내적값을 알고 있는 것 아닌가요? 그래도, 우리 두 가지는 꽤 직관적으로 알 수 있습니다.

$$\vec{v}\cdot\vec{v}=|\vec{v}|^2$$

$$\vec{v}\cdot\vec{w}=\vec{w}\cdot\vec{v}$$

우리가 하고 싶은 일은 두 이동 $\vec{v}$와 $\vec{w}$이 이루는 각도를 몰라도 두 이동이 이루는 각도를 구하는 것입니다.

 

이번엔 조금 다른 이야기를 해 보고자 합니다. 어떤 기저 $\beta=\left\{\hat{i}, \hat{j}\right\}$로 나타낸 다음과 같은 두 이동이 있다고 해 봅시다.

$$\vec{v}=a\hat{i}+b\hat{j}$$

$$\vec{w}=c\hat{i}+d\hat{j}$$

여기에 다음이 만족하는 같이 분배법칙이 성립하는 꽤 직관적인 연산을 줘 보고 싶습니다.

$$\vec{v}\cdot\vec{w}=(a\hat{i}+b\hat{j})\cdot(c\hat{i}+d\hat{j})=ac\hat{i}\cdot\hat{i}+bc\hat{j}\cdot\hat{i}+ad\hat{i}\cdot\hat{j}+bd\hat{i}\cdot\hat{j}$$

이 연산이 위에서 논한 두 가지 내적의 성질을 가지도록 하고 싶습니다. 첫 성질은 나중에 다뤄보고, 두번째 성질 (대칭성)을 만족하기 위해서는 (조금 연산을 생략하겠지만) 다음을 만족해야 합니다!

$$\hat{i}\cdot\hat{j}=\hat{j}\cdot\hat{i}$$

즉, 다음처럼 정리가 됩니다.

$$\vec{v}\cdot\vec{w}=ac\hat{i}\cdot\hat{i}+(ad+bc)\hat{i}\cdot\hat{j}+bd\hat{i}\cdot\hat{j}$$

이제, 첫 성질을 만족하도록 하고 싶습니다. 한번 두 이동의 합의 크기를 생각해봅시다.

$$|\vec{v}+\vec{w}|^2=(\vec{v}+\vec{w})\cdot(\vec{v}+\vec{w})=\vec{v}\cdot\vec{v}+2\vec{v}\cdot\vec{w}+\vec{w}\cdot\vec{w}$$

그런데, 다시 코사인 법칙을 생각해 보면, 여기서 

$$\vec{v}\cdot\vec{w}=|\vec{v}||\vec{w}|\cos\theta$$

를 만족해야 함을 알 수 있습니다.

 

그런데, $\vec{v}\cdot\vec{w}$의 값은 기저간의 내적 값만 미리 알고 있다면, 좌표 표현에서 어렵지 않게 구할 수 있습니다. 예를 들어봅시다! 맨 처음 직각 격자에서 구한 이동의 크기를 생각해봅시다. 위에서 얘기한 내용을 다 모으면, 다음과 같은 것은 어렵지 않게 떠올려낼 수 있습니다!

$$[\vec{v}]_\beta=\pmatrix{a\\b}$$

$$\vec{v}\cdot\vec{v}=a^2\hat{i}\cdot\hat{i}+2ab\hat{i}\cdot\hat{j}+b^2\hat{i}\cdot\hat{j}$$

그런데, 이 직각 격자에서는 $\vec{v}\cdot\vec{v}$의 값이 $a^2+b^2$이어야 합니다. 그렇다면, 기저 간의 내적은 다음과 같을 것입니다.

$$\hat{i}\cdot\hat{i}=\hat{j}\cdot\hat{j}=1$$

$$\hat{i}\cdot\hat{j}=0$$

이러한 기저를 정규직교기저(Orthonormal basis)라 부릅니다! 같은 기저를 내적하면 1이고, 다른 기저를 내적하면 0이 나오는 것이죠. 이제 이는 위에서 코사인으로 한 정의와도 같습니다. 모든 기저의 크기는 1이었고, 기저 간에는 수직이었죠. 

이제, 이 정규직교기저로 표현한 다음과 같은 두 이동

$$[\vec{v}]_\beta=\pmatrix{v^1\\v^2}, [\vec{w}]_\beta=\pmatrix{w^1\\w^2}$$

의 내적은 다음과 같이 표현할 수 있습니다.

$$\vec{v}\cdot\vec{w}=v^1w^1+v^2w^2$$

(왜 굳이 윗첨자일까요? 이에 대해서는 다음 글에서 얘기해봅시다!)

 

혹은, 그 다음에 제시한 삐뚤어진 격자에서도 마찬가지 방법으로 내적을 구해볼 수 있습니다.

$\beta^\prime$으로 표현한 이동의 크기는 다음과 같이 구할 수 있었지요.

$$\vec{v}_{\beta^\prime}=\pmatrix{a\\b}$$

$$|\vec{v}|^2=2a^2+5b^2-2ab$$

이제, 마찬가지 과정으로 기저 간의 내적을 구해보면 다음과 같습니다.

$$\hat{i}^\prime\cdot\hat{i}^\prime=2$$

$$\hat{j}^\prime\cdot\hat{j}^\prime=5$$

$$\hat{i}^\prime\cdot\hat{j}^\prime=-1$$

이도 마찬가지로 위의 삐뚫어진 격자에서 처음 말한 코사인을 이용한 정의로 직접 구할 수 있습니다. 

$\hat{i}^\prime$의 크기는 $\sqrt{5}$였고, $\hat{j}^\prime$의 크기는 $\sqrt{2}$였죠.

결국, $\beta^\prime$으로 나타낸 이동

$$[\vec{v}]_{\beta^\prime}=\pmatrix{v^1\\v^2},[\vec{w}]_{\beta^\prime}=\pmatrix{w^1\\w^2}$$

의 내적은 다음과 같이 표현할 수 있습니다.

$$\vec{v}\cdot\vec{w}=5v^1w^1-(v^1w^2+v^2w^1)+2v^2w^2$$

 

멀리 돌아왔지만, 결론은 기저 간의 내적 값만 알고 있다면, 이 기저로 표현한 임의의 두 이동의 내적을 구할 수 있다는 것입니다! 이렇게 기저에 부여된 내적을 계량(metric)이라 부릅니다. 그런데, 애초에 기저의 내적을 격자를 보면 구할 수 있는데 조금 돌아 온 느낌이 있는 것 같습니다. 그렇지만 격자를 항상 우리가 눈으로 볼 수 있는건 아니잖아요? 조금 더 재밌는 논의를 해볼 수 있습니다.

$\mathbb{R}$-벡터공간 $V$에 이항 연산 $\left<\cdot,\cdot\right>:V\times V \rightarrow \mathbb{R}$가 주어졌다고 하자.
이 때, 임의의 $u,v,w \in V$ 가 다음을 모두 만족한다. 
 1. $\left< v,w \right>=\left< w,v \right>$ (대칭성)
 2. $\left< au+bv,w \right>=a\left< u,w \right>+b\left< v,w \right>$ (선형성)
 3. $0$이 아닌 $v$에 대해, $\left<v,v\right> > 0$ (양의 정부호)
이 때, 연산 $\left<\cdot,\cdot\right>$을 내적이라 부른다.

이렇게 내적이라는 연산이 임의의 벡터 공간에 부여되면, 내적이라는 연산은 다음과 같은 대칭 이차 형식으로 표현 가능합니다. (여기선 이차 형식이 대칭이라는 말은, $[g]_\beta$가 대칭행렬이라는 말이 됩니다.)

$$\left< v,w \right>=[v]_\beta ^T [g]_\beta [w]_\beta$$

 

예를 들어, 첫 번째 직각 격자에서의 내적은 다음과 같이 표현됩니다.

$$[\vec{v}]_\beta=\pmatrix{v^1\\v^2}, [\vec{w}]_\beta=\pmatrix{w^1\\w^2}$$

$$\left< \vec{v},\vec{w} \right>=\pmatrix{v^1 & v^2}\pmatrix{1 & 0 \\ 0 & 1}\pmatrix{w^1\\w^2}$$

 

마찬가지로, 두 번째 비뚤어진 격자에서의 내적은 다음과 같이 표현할 수 있습니다.

$$[\vec{v}]_{\beta^\prime}=\pmatrix{v^1\\v^2},[\vec{w}]_{\beta^\prime}=\pmatrix{w^1\\w^2}$$

$$\left< \vec{v},\vec{w} \right>=\pmatrix{v^1 & v^2}\pmatrix{5 & -1 \\ -1 & 2}\pmatrix{w^1\\w^2}$$

 

즉, 이 행렬 $[g]_\beta$는 기저의 내적값을 담고 있습니다. 정확히 말하면, 기저가 다음과 같이 주어지면,

$$\beta=\left\{ e_1,e_2,\cdots,e_n \right\}$$

$[g]_\beta$는 다음과 같은 성분을 가지는 행렬입니다. 

$$g_{ij} = \left< e_i,e_j \right>$$

위에 이동에 대입해보면, 당연히 대칭행렬이어야 하겠죠!

 

그렇다면, 애초에 어떤 벡터공간에 계량 $g$를 주는 것으로 우리는 그 벡터공간에 새로운 격자를 만들어낼 수 있습니다! 그러니까, 애초에 각도와 크기를 다음과 같이 정의해 버리는것이죠!

$\mathbb{R}$-벡터공간 $V$에 두 벡터 간의 내적 $\left<\cdot,\cdot\right>$이 주어졌다고 하자. 
$V$의 원소 $v, w$에 대해, 
$$||v||=\sqrt{\left< v,v \right>}$$
를 $v$의 크기라 정의하고,
$$\cos\theta=\frac{\left< v,w \right>}{||v|| ||w||}$$
를 만족하는 $\theta$를 $v$와 $w$사이의 각도라 정의한다.

이제, 벡터 공간에 적절한 계량을 부여해주는 것 만으로, 우리는 일반적인 벡터 공간을 지금까지 열심히 논의한 이동처럼 다룰 수 있게 됐습니다.

 

즉, ($\mathbb{R}$)벡터 공간은 애초에 실수 순서쌍일 뿐이었는데, 우리가 어떤 계량이라는 것을 주면 여기에 크기라는 것을 줄 수 있다는 것이죠. 예를 들어

$$(1,3)$$

이라는 순서쌍이 있었는데, 여기에 우리가 다음과 같은 격자를 심어줬다면

$$\pmatrix{1&3\\3&2}$$

이 순서쌍의 '크기'가 37이 되는 것을 알 수 있는 것이죠! 

 

우리가 앞으로 다룰 벡터는 이 이동처럼 움직이는, 적절한 계량이 주어진 벡터 공간입니다. 다음 시간에는 공간 위에 벡터를 어떻게 잘 적용할지, 정확히는- 공간을 표현하는 방법인 좌표계에 대해 얘기해보도록 합시다!