안녕하세요! 서울대감자입니다.
그동안 선형대수학의 기초라는 딱딱한 주제의 글만 10개 넘게 썼는데요,
이번에는 색다른 컨텐츠를 준비해봤습니다.
우리는 축전기를 어떻게 배웠나요? 아마 대부분 극판의 넓이가 극판 사이의 감격보다 매우 크다면 전하가 거의 고르게 분포하게 된다고 베웠을 것입니다. 하지만 여기서 의문이 생기지 않나요? 그러면 정확히 어떤 분포를 띠는지.
그래서 이번 글에서는 제목에서도 알 수 있듯이
정사각형 축전기의 전하 밀도를 코딩으로 구해보자!
라는 주제를 가지고 왔습니다. 이 주제로는 총 2개의 글을 쓸 예정이며, 이번 글에서는 코딩 아이디어와, 이 코드가 실제로 결과를 어떻게 내는지 살펴보겠습니다. 사용 언어는 C++입니다.
1. 아이디어
(1단계) 먼저 정사각형 금속판 2개를 $\texttt{size} \times \texttt{size}$ 격자로 나눠주고 하나의 판에는 모든 격자에 동일한 전하 $\texttt{1}$, 나머지 판에는 모든 격자에 동일한 전하 $\texttt{-1}$만큼 체워줍시다. 그리고 두께 $\texttt{thickness}$를 지정합니다.
(2단계) 각각의 그리드의 면전하가 받는 전기력의 크기를 계산합니다.
$$\mathbf{F} = \frac{1}{4 \pi \epsilon_0} \frac{q_1q_2}{r^2}\hat{\mathbf{r}}$$
에서 편의를 위해 상수항 $\dfrac{1}{4 \pi \epsilon_0}$은 무시합니다.
(3단계) 2단계에서 전하에 작용하는 힘을 구했으니 이제는 그 전기력에 따라 전하를 움직여야 합니다. 전하를 움직이는 규칙은 다음과 같이 합시다.
- 전하가 판을 빠져나가지 않습니다.
- $\texttt{[i][j]}$에 있는 전하가 받는 힘의 $\texttt{x}$축 방향 성분 $\texttt{F_x}$가 양수면 $\texttt{[i+1][j]}$로 전하가 $\texttt{F_x}$에 비례하는 만큼 이동하고, $\texttt{F_x}$가 음수면 $\texttt{[i-1][j]}$로 전하가 $\texttt{-F_x}$에 비례하는 만큼 이동한다.
- $\texttt{[i][j]}$에 있는 전하가 받는 힘의 $\texttt{y}$축 방향 성분 $\texttt{F_y}$가 양수면 $\texttt{[i][j+1]}$로 전하가 $\texttt{F_y}$에 비례하는 만큼 이동하고, $\texttt{F_y}$가 음수면 $\texttt{[i][j-1]}$로 전하가 $\texttt{-F_y}$에 비례하는 만큼 이동한다.
(4단계) 2단계와 3단계를 반복하는 $\texttt{for}$문을 짭니다.
(5단계) 텍스트 파일에 전하량 정보를 출력합니다.
1단계부터 5단계를 모두 반영한 코드는 다음과 같습니다.
#include <iostream>
#include <fstream>
#include <cmath>
using namespace std;
int signal(double a) {
if (a > 0) return 1;
if (a == 0) return 0;
if (a < 0) return -1;
}
// 3단계
int main() {
const int size = 30;
double thickness = 10;
double plane1[size][size];
double plane2[size][size];
double temp_plane1[size][size];
double temp_plane2[size][size];
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
plane1[i][j] = 1;
plane2[i][j] = -1;
temp_plane1[i][j] = 1;
temp_plane2[i][j] = -1;
}
}
// 1단계
const double ratio = 0.01; // 3단계
int final_time = 1000; // 4단계
// This line is intentionally left blank. - (1)
for (int time = 0; time < final_time; time++) {
//plane1
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
double F_x = 0;
double F_y = 0;
//plane1 and plane2
for (int i1 = 0; i1 < size; i1++) {
for (int j1 = 0; j1 < size; j1++) {
double distance = sqrt(pow((i - i1), 2) + pow((j - j1), 2) + pow(thickness, 2));
F_x -= plane1[i][j] * plane2[i1][j1] * (i1 - i) / pow(distance, 3);
F_y -= plane1[i][j] * plane2[i1][j1] * (j1 - j) / pow(distance, 3);
temp_F_z += plane1[i][j] * plane2[i1][j1] * thickness / pow(distance, 3);
}
}
//plane1 and plane1
for (int i1 = 0; i1 < size; i1++) {
for (int j1 = 0; j1 < size; j1++) {
double distance = sqrt(pow((i - i1), 2) + pow((j - j1), 2));
if (distance != 0) {
F_x -= plane1[i][j] * plane1[i1][j1] * (i1 - i) / pow(distance, 3);
F_y -= plane1[i][j] * plane1[i1][j1] * (j1 - j) / pow(distance, 3);
}
}
}
// 2단계
double moved_charge = 0;
bool x_exist = false;
bool y_exist = false;
if ((i + signal(F_x)) < size && (i + signal(F_x)) > -1) x_exist = true;
if ((j + signal(F_y)) < size && (j + signal(F_y)) > -1) y_exist = true;
temp_plane1[i + x_exist * signal(F_x)][j] += x_exist * fabs(F_x) * ratio;
moved_charge += x_exist * fabs(F_x) * ratio;
temp_plane1[i][j + y_exist * signal(F_y)] += y_exist * fabs(F_y) * ratio;
moved_charge += y_exist * fabs(F_y) * ratio;
temp_plane1[i][j] -= moved_charge;
// 3단계
// This line is intentionally left blank. - (2)
}
}
//plane2
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
double F_x = 0;
double F_y = 0;
//plane2 and plane1
for (int i1 = 0; i1 < size; i1++) {
for (int j1 = 0; j1 < size; j1++) {
double distance = sqrt(pow((i - i1), 2) + pow((j - j1), 2) + pow(thickness, 2));
F_x -= plane2[i][j] * plane1[i1][j1] * (i1 - i) / pow(distance, 3);
F_y -= plane2[i][j] * plane1[i1][j1] * (j1 - j) / pow(distance, 3);
}
}
//plane2 and plane2
for (int i1 = 0; i1 < size; i1++) {
for (int j1 = 0; j1 < size; j1++) {
double distance = sqrt(pow((i - i1), 2) + pow((j - j1), 2));
if (distance != 0) {
F_x -= plane2[i][j] * plane2[i1][j1] * (i1 - i) / pow(distance, 3);
F_y -= plane2[i][j] * plane2[i1][j1] * (j1 - j) / pow(distance, 3);
}
}
}
// 2단계
double moved_charge = 0;
bool x_exist = false;
bool y_exist = false;
if ((i + signal(F_x)) < size && (i + signal(F_x)) > -1) x_exist = true;
if ((j + signal(F_y)) < size && (j + signal(F_y)) > -1) y_exist = true;
temp_plane2[i + x_exist * signal(F_x)][j] -= x_exist * fabs(F_x) * ratio;
moved_charge -= x_exist * fabs(F_x) * ratio;
temp_plane2[i][j + y_exist * signal(F_y)] -= y_exist * fabs(F_y) * ratio;
moved_charge -= y_exist * fabs(F_y) * ratio;
temp_plane2[i][j] -= moved_charge;
// 3단계
}
}
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
plane1[i][j] = temp_plane1[i][j];
plane2[i][j] = temp_plane2[i][j];
}
}
// 2단계와 3단계가 모두 끝난 뒤 plane1, plane2 갱신
cout << time + 1 << " "; // 진행상황 표시
}
// 4단계
ofstream fout;
fout.open("Conductor.txt");
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
fout << plane1[i][j] << " ";
}
fout << "\n";
}
fout << "\n";
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
fout << plane2[i][j] << " ";
}
fout << "\n";
}
// This line is intentionally left blank. - (3)
fout.close();
// 5단계
cout << "END";
return 0;
}
위 코드에서는 총 1000번 2단계와 3단계를 반복하도록 코드를 짰습니다. 그런데 의문이 하나 들지 않나요? 1000번 반복 계산하여 얻은 결과는 전하에 작용하는 힘의 크기가 충분히 0에 가깝다고 할 수 있을지요. 그렇다면 0에 충분히 가깝다의 기준은 어떻게 잡아야 할까요?
저는 각 그리드마다 (1000번 지난 후 전하에 작용하는 힘의 크기)/(초기 상태에서 전하에 작용하는 힘의 크기)를 구해서 가장자리를 제외한 영역에서 이 값이 0.01보다 작으면 0에 충분히 가깝다고 할 수 있다고 가정했습니다. 그래서 힘의 크기의 비율을 확인하기 위해 다음과 같은 코드를 추가하였습니다.
// This line is intentionally left blank. - (1)
double initial_force[size][size];
double final_force[size][size];
// This line is intentionally left blank. - (2)
if (time == 0) initial_force[i][j] = sqrt(pow(acc_x, 2) + pow(acc_y, 2));
if (time == final_time - 1) final_force[i][j] = sqrt(pow(acc_x, 2) + pow(acc_y, 2));
// This line is intentionally left blank. - (3)
fout << "\n";
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
if (initial_force[i][j] != 0) fout << final_force[i][j] / initial_force[i][j] << " ";
else fout << 100 << " ";
}
fout << "\n";
}
2. 실행 결과
이제 위의 코드를 실행시켜 전하밀도를 구해봅시다.
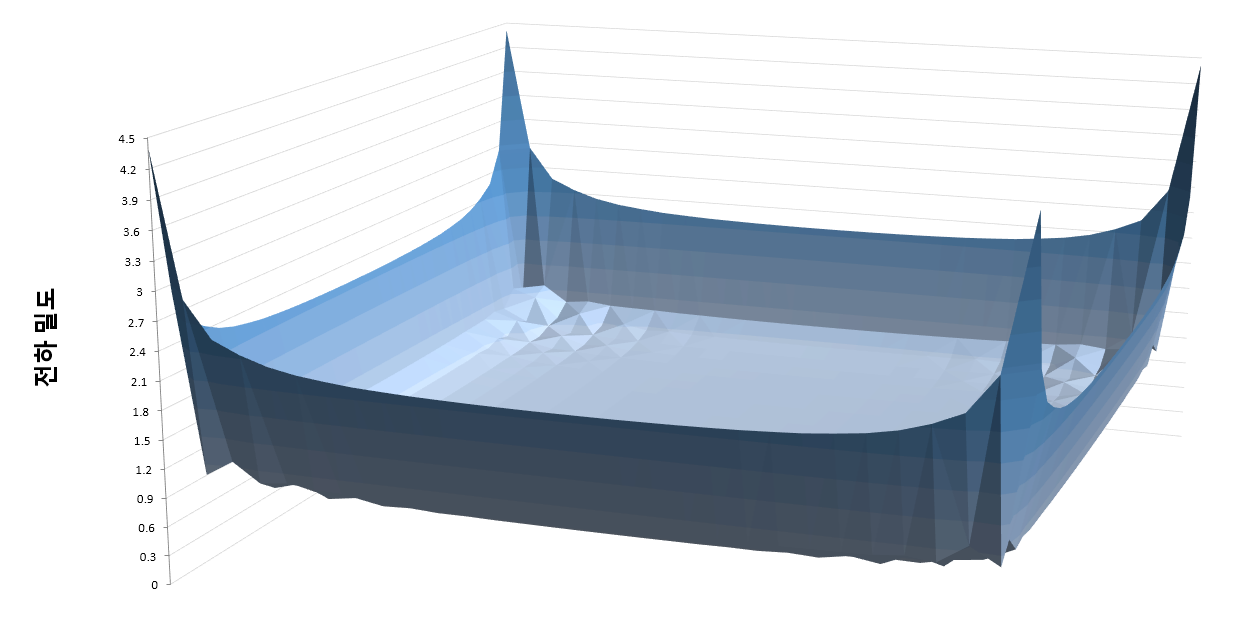
약간 울퉁불퉁하지만 전체적으로 중심에서는 전하가 고르게 퍼져 있고, 가장자리로 갈수록 전하밀도가 급격히 증가하는 형태를 띱니다. (1000번 지난 후 전하에 작용하는 힘의 크기)/(초기 상태에서 전하에 작용하는 힘의 크기)는 다음과 같습니다.

붉게 칠한 부분이 0.01 이상인 곳인데, 붉은 영역이 매우 적어 힘의 평형이 도달했다고 판단해도 무방한 수준입니다.
여기서 호기심이 생겼습니다. 1500번, 2000번 반복하면 결과가 어떻게 나올까? 더 좋은 결과가 나올까? 결과는 다음과 같았습니다.
1500번 반복


2000번 반복


횟수가 늘어나면서 그래프가 울퉁불퉁해지고, (n번 지난 후 전하에 작용하는 힘의 크기)/(초기 상태에서 전하에 작용하는 힘의 크기)가 0.01인 곳이 늘어났습니다.
이유는 알 수 없지만, 두께가 10일 때는 전하에 작용하는 힘의 크기는 횟수가 늘어날 수록 줄어들다가 다시 증가하는 양상을 보였습니다. 아래 표는 가장자리를 제외한 28×28개의 그리드에서 (n번 지난 후 전하에 작용하는 힘의 크기)/(초기 상태에서 전하에 작용하는 힘의 크기)의 합을 나타낸 것입니다.
| n | 500 | 700 | 1000 | 1500 | 2000 |
| $\displaystyle \sum \dfrac{F_f}{F_i}$ | 25.41 | 7.110 | 2.264 | 3.346 | 4.499 |
$\displaystyle \sum \dfrac{F_f}{F_i}$가 최소가 될 때가 실제 전하밀도와 가장 유사한 시점이라고 생각할 수 있을 것입니다.
다음 시간에는 $\displaystyle \sum \dfrac{F_f}{F_i}$가 최소가 될 때까지(좀 더 정확히는 극소가 될 때까지)만 연산 과정을 반복하는 코드를 짜보겠습니다. 그리고 축전기 두께를 바꾸어 보고, 축전기 사이에 작용하는 힘의 크기를 계산하여 실제 이론과 비교해보겠습니다.
'물리학 > 전자기학' 카테고리의 다른 글
| 11. Epilogue (0) | 2022.08.01 |
|---|---|
| 10. 맥스웰 방정식, 전자기파 방사 (0) | 2022.08.01 |
| 9. 전자기 유도, 자기 에너지 (0) | 2022.07.31 |
| 8. 물질 속 자기장, 자기장 세기 (0) | 2022.07.30 |
| 7. 자기 퍼텐셜 (0) | 2022.07.28 |
