이번 시간에는 행렬식의 성질을 배워보겠습니다.
$\mathrm{det}(A)=\mathrm{det}(A^t)$
행렬식의 정의에 의해
$$\begin{aligned} \mathrm{det}(A^t) & = \displaystyle \sum_{\sigma \in S_n} \mathrm{sgn}(\sigma)(A^t)_{1 \sigma(1)} (A^t)_{2 \sigma(2)} \cdots (A^t)_{n \sigma(n)} \\ & = \displaystyle \sum_{\sigma \in S_n} \mathrm{sgn}(\sigma)a_{\sigma(1) 1} a_{\sigma(2) 2} \cdots a_{\sigma(n) n} \end{aligned}$$
입니다. 한편
$$ a_{\sigma(1) 1} a_{\sigma(2) 2} \cdots a_{\sigma(n) n} = a_{1 \sigma^{-1}(1)} a_{2 \sigma^{-1}(2)} \cdots a_{n \sigma^{-1}(n)} $$
이고, (1-40)에 의해
$$\begin{aligned} \mathrm{det}(A^t) & = \displaystyle \sum_{\sigma \in S_n} \mathrm{sgn}(\sigma)a_{\sigma(1) 1} a_{\sigma(2) 2} \cdots a_{\sigma(n) n} \\ & = \displaystyle \sum_{\sigma^{-1} \in S_n} \mathrm{sgn}(\sigma^{-1}) a_{1 \sigma^{-1}(1)} a_{2 \sigma^{-1}(2)} \cdots a_{n \sigma^{-1}(n)} \\ & =\mathrm{det}(A) \end{aligned}$$
입니다.
아래 성질은 어떤 행렬의 행렬식은 전치행렬의 행렬식과 같다는 것에서 유도되는 성질들입니다. (1-41)과 비교해보세요.
행렬 $A=(a_1 \, a_2 \, \cdots \, a_n)$에 대하여
- (교대성1) $i \neq j$일 때 $a_i = a_j$이면 $\mathrm{det}(A)=0$이다.
- (다중선형성) 행렬식은 각 열에 대해서 선형성을 갖는다. $a_i = v_1 + cv_2$면 $$\begin{array}{l} \mathrm{det}(a_1 \, \cdots \, a_i \, \cdots \, a_n) \\ =\mathrm{det}(a_1 \, \cdots \, v_1+cv_2 \, \cdots \, a_n) \\ =\mathrm{det}(a_1 \, \cdots \, v_1 \, \cdots \, a_n) + c \, \mathrm{det}(a_1 \, \cdots \, v_2 \, \cdots \, a_n) \end{array}$$
- 한 열에 다른 열의 상수배를 더해도 행렬식의 값은 변하지 않는다. 즉, $$\begin{array}{l} \mathrm{det} (a_1 \, \cdots \, a_1 \, \cdots \, a_j \, \cdots \, a_n) \\ =\mathrm{det}(a_1 \, \cdots \, a_i+ca_j \, \cdots \, a_j \, \cdots \, a_n) \end{array}$$
- (교대성2) 두 열의 위치를 바꾸면 부호가 바꾼다. $$\begin{array}{l} \mathrm{det}(a_1 \, \cdots \, a_i \, \cdots \, a_j \, \cdots \, a_n) \\ =-\mathrm{det}(a_1 \, \cdots \, a_j \, \cdots \, a_i \, \cdots \, a_n) \end{array}$$
이제 행렬식을 쉽게 구할 수 있는 몇 가지 방법을 소개하겠습니다.
$n \times n$ 행렬의 $i$번째 행과 $j$번째 행을 지운 행렬을 $\tilde {A}_{ij}$라 하자. $n \geq 2$일 때 행렬식은 다음과 같이 계산된다.
$$\mathrm{det}(A) = \displaystyle \sum_{i=1}^{n}a_{ij}(-1)^{i+j}\mathrm{det}{\tilde{A}_{ij}}$$
$$\mathrm{det}(A) = \displaystyle \sum_{j=1}^{n}a_{ij}(-1)^{i+j}\mathrm{det}{\tilde{A}_{ij}}$$
이를 라플라스 전개라고 부른다.
$\tilde{A}_{ij}$의 개념을 확실히 하고 가는 게 좋을 것 같네요. 행렬
$$A=\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}$$
에 대하여
$$\tilde{A}_{12} = \begin{pmatrix} 4 & 6 \\ 7 & 9 \end{pmatrix}$$
$$\tilde{A}_{23} = \begin{pmatrix} 1 & 2 \\ 7 & 8 \end{pmatrix}$$
입니다. 이제
$$\mathrm{det}(A) = \displaystyle \sum_{i=1}^{n}a_{ij}(-1)^{i+j}\mathrm{det}{\tilde{A}_{ij}}$$
를 $n$에 대한 수학적 귀납법을 이용하여 증명해보겠습니다.
먼저 $n=2$일 때를 살펴봅시다. 먼저 행렬식 정의에 의하면
$$\begin{aligned} \mathrm{det}(A) & =\displaystyle \sum_{\sigma \in S_{2}} \mathrm{sgn}(\sigma) a_{1 \sigma(1)} a_{2 \sigma(2)} \\ & = \mathrm{sgn}\begin{pmatrix} 1 & 2 \\ 1 & 2 \end{pmatrix} a_{11}a_{22} + \mathrm{sgn}\begin{pmatrix} 1 & 2 \\ 2 & 1 \end{pmatrix} a_{12}a_{21} \\ & = a_{11}a_{22} - a_{12}a_{21} \end{aligned}$$
라플라스 전개에 대해서 살펴봅시다. $j=1$이라 하면
$$\begin{aligned} \mathrm{det}(A) & = \displaystyle \sum_{i=1}^{2} a_{i1} (-1)^{i+1}\mathrm{det}{\tilde{A}_{i1}} \\ & = a_{11} (-1)^{2} a_{22} + a_{21} (-1)^{3} a_{12} = a_{11}a_{22} - a_{12}a_{21} \end{aligned}$$
로 행렬식의 정의와 같은 결과가 나오는 것을 확인할 수 있습니다. $j=2$일 때는 직접 해보시기 바랍니다.
다음으로 $(n-1) \times (n-1)$ 행렬일 때 라플라스 전개가 성립한다고 가정하고 $n \times n$ 행렬에서도 라플라스 전개가 성립하는지 살펴봅시다.
행렬식의 정의에 의하면$$\mathrm{det}(A) = \sum_{\sigma \in S_n} \mathrm{sgn}(\sigma) a_{1 \sigma(1)} a_{2 \sigma(2)} \cdots a_{n \sigma(n)}$$이고, 이 식은 다음과 같이 변형할 수 있습니다. ($(S_n)_{ij}$는 $\sigma(i)=j$인 치환의 집합)$$\sum_{i=1}^{n}a_{ij} \sum_{\sigma \in (S_n)_{ij}} \mathrm{sgn}(\sigma) a_{1 \sigma(1)} \cdots a_{(i-1) \sigma(i-1)} a_{(i+1)\sigma(i+1)} \cdots a_{n \sigma(n)}$$$\sigma \in (S_n)_{ij}$와 $\sigma' \in S_{n-1}$ 사이에는 다음과 같은 일대일 대응이 존재합니다.$$\sigma'(k) = \left\{ \begin{matrix} \sigma(k) & (k<i, \, \sigma(k)<j) \\ \sigma(k)-1 & (k<i, \, \sigma(k) > j) \\ \sigma(k-1) & (k>i, \, \sigma(k) < j) \\ \sigma(k-1)-1 & (k>i, \, \sigma(k) > j) \end{matrix} \right.$$따라서
$$\begin{array}{l} \displaystyle \sum_{i=1}^{n}a_{ij} \sum_{\sigma \in (S_n)_{ij}} \mathrm{sgn}(\sigma) a_{1 \sigma(1)} \cdots a_{(i-1) \sigma(i-1)} a_{(i+1)\sigma(i+1)} \cdots a_{n \sigma(n)} \\ = \displaystyle \sum_{i=1}^{n} a_{ij} \sum_{\sigma' \in S_{n-1}} \mathrm{sgn}(\sigma) (\tilde{A}_{ij})_{1 \sigma'(1)} (\tilde{A}_{ij})_{2 \sigma'(2)} \cdots (\tilde{A}_{ij})_{(n-1) \sigma'(n-1)} \end{array}$$
$\mathrm{sgn}(\sigma)$와 $\mathrm{sgn}(\sigma')$ 사이의 관계를 살펴봅시다. 치환 $\sigma$의 전도의 수는 $\sigma(k+1)$부터 $\sigma(n)$까지 중에 $\sigma(k)$보다 작은 것의 개수 $N_k$를 $1 \leq k \leq n-1$에 대해서 모두 더한 것입니다.
$$N(\sigma) = N_1 + N_2 + \cdots + N_{n-1}$$
그리고 치환 $\sigma'$의 전도의 수는 $\sigma(1)$부터 $\sigma(i-1)$까지 중에서 $j$보다 큰 값의 개수 $N'$에 대하여
$$\begin{aligned} N(\sigma') & = (N_1 + N_2 + \cdots + N_{i-1} - N') + (N_{i+1} + \cdots N_{n-1}) \\ & =N(\sigma) - (N_i + N') \end{aligned}$$
입니다. 아래 그림에서 알 수 있듯이 $N_i$는 $i+1 \leq k \leq n$, $\sigma(k) < j$인 $k$의 개수로,
$$N_i = j-i+N'$$
입니다.

따라서 $N(\sigma') = N(\sigma) - 2N' + (i-j)$이고,
$$\mathrm{sgn}(\sigma') = (-1)^{i-j} \mathrm{sgn}(\sigma) = (-1)^{i+j} \mathrm{sgn}(\sigma)$$
입니다. 그러므로
$$\begin{array}{l} \displaystyle \sum_{i=1}^{n} a_{ij} \sum_{\sigma' \in S_{n-1}} \mathrm{sgn}(\sigma) (\tilde{A}_{ij})_{1 \sigma'(1)} (\tilde{A}_{ij})_{2 \sigma'(2)} \cdots (\tilde{A}_{ij})_{(n-1) \sigma'(n-1)} \\ = \displaystyle \sum_{i=1}^{n} a_{ij}(-1)^{i+j} \sum_{\sigma' \in S_{n-1}} \mathrm{sgn}(\sigma') (\tilde{A}_{ij})_{1 \sigma'(1)} (\tilde{A}_{ij})_{2 \sigma'(2)} \cdots (\tilde{A}_{ij})_{(n-1) \sigma'(n-1)} \end{array}$$
이고, 귀납 가정에 의해 최종적으로 다음을 얻습니다.
$$\mathrm{det}(A) = \displaystyle \sum_{i=1}^{n}a_{ij}(-1)^{i+j}\mathrm{det}{\tilde{A}_{ij}}$$
이로써 증명을 마칩니다.
$$\mathrm{det}(A) = \displaystyle \sum_{j=1}^{n}a_{ij}(-1)^{i+j}\mathrm{det}{\tilde{A}_{ij}}$$
도 비슷하게 증명할 수 있습니다.
정사각행렬 $A$에 대하여 $i>j$일 때 $(A)_{ij}=0$인 행렬을 상삼각행렬이라고 하고, $i<j$일 때 $(A)_{ij}=0$인 행렬을 하삼각행렬이라 한다. 상삼각행렬과 하삼각행렬을 아울러 삼각행렬이라고 한다.
삼각행렬 $A$의 대각성분을 $\lambda_1$, $\lambda_2$, $\cdots$, $\lambda_n$이라 하면 $\mathrm{det}(A) = \lambda_1 \lambda_2 \cdots \lambda_n$이다.
라플라스 전개를 이용하든 행렬식의 정의를 이용하든 증명은 어렵지 않으니 스스로 해보시기 바랍니다.
이 방법은 행렬에 기본행렬연산을 적용하여 삼각행렬로 만든 뒤 대각성분만 곱하면 된다는 점을 말해줍니다. 예를 들어
$$A = \begin{pmatrix} 2 & 1 & 3 \\ 1 & 3 & -1 \\ 4 & -2 & 2 \end{pmatrix}$$
의 행렬식을 구하기 위해 주어진 행렬을 상삼각행렬로 바꿀 것입니다.
(1단계) 2행에 1행의 $-\dfrac{1}{2}$배, 3행에 1행의 -2배를 더합니다.
$$\begin{pmatrix} 2 & 1 & 3 \\ 0 & \dfrac{5}{2} & -\dfrac{5}{2} \\ 0 & -4 & -4 \end{pmatrix}$$
(2단계) 3행에 2행의 $\dfrac{8}{5}$배를 더합니다.
$$\begin{pmatrix} 2 & 1 & 3 \\ 0 & \dfrac{5}{2} & -\dfrac{5}{2} \\ 0 & 0 & -8 \end{pmatrix}$$
상삼각행렬이 완성되었고, 대각성분이 $2$, $\dfrac{5}{2}$, $-8$이므로 행렬식의 값은 $-40$입니다. 라플라스 전개나 행렬식의 정의로 구한 값과 비교해보세요.
$3 \times 3$ 행렬에서는 이 방법의 편의성을 느끼지 못할 지도 모르겠습니다. 하지만 이 방법의 진가는 행렬의 크기가 커질 때 나타납니다. $6 \times 6$ 행렬을 아무렇게나 하나 만들어보고 행렬식의 정의를 이용하는 방법, 라플라스 전개를 이용하는 방법, 삼각행렬을 만드는 방법 중 어느 것이 더 편리한지 확인해보세요. 아마 삼각행렬을 이용하는 것이 행렬식의 정의나 라플라스 전개를 이용하는 방법보다 대략 10배 정도 빠를 겁니다.
- 행렬 $M = \begin{pmatrix} A & B \\ O & I \end{pmatrix}$의 행렬식은 $\mathrm{det}(A)$이다. (단, $A$는 정사각행렬)
- 행렬 $M = \begin{pmatrix} I & O \\ A & B \end{pmatrix}$의 행렬식은 $\mathrm{det}(B)$이다. (단, $B$는 정사각행렬)
- 행렬 $M = \begin{pmatrix} A & B \\ O & C \end{pmatrix}$의 행렬식은 $\mathrm{det}(A) \mathrm{det}(C)$이다. (단, $A$, $C$는 정사각행렬)
- 기본행연산을 통해 $M = \begin{pmatrix} A & B \\ O & I_{n-m} \end{pmatrix}$은 $M' = \begin{pmatrix} A & O \\ O & I_{n-m} \end{pmatrix}$로 바꿀 수 있습니다. $M'$의 행렬식은 $\sigma(k)=k(m + 1 \leq k \leq n)$인 치환의 집합 $S_n '$에 대하여(단, $M$의 한 변의 크기는 $n$) $$\begin{array}{l} \displaystyle \sum_{\sigma \in S_n} \mathrm{sgn}(\sigma)a_{1 \sigma(1)} a_{2 \sigma(2)} \cdots a_{n \sigma(n)} \\ = \displaystyle \sum_{\sigma \in S_n '} \mathrm{sgn}(\sigma) a_{1 \sigma(1)} a_{2 \sigma(2)} \cdots a_{m \sigma(m)} \\ = \displaystyle \sum_{\sigma \in S_m} \mathrm{sgn}(\sigma)a_{1 \sigma(1)} a_{2 \sigma(2)} \cdots a_{m \sigma(m)} \end{array}$$이므로 $\mathrm{det}(M') = \mathrm{det}(A)$이고, 따라서 $\mathrm{det}(M) = \mathrm{det}(A)$입니다.
- 1번과 비슷하게 증명 가능합니다.
- $C$가 비가역이면 $\mathrm{det}(C)=0$이고, $M$의 행은 일차종속이므로 $\mathrm{det}(M) = 0$입니다. 따라서 $\mathrm{det}(M) = \mathrm{det}(A) \mathrm{det}(C)$입니다. $C$가 가역이라고 합시다. 그러면 $M' = \begin{pmatrix} I & O \\ O & C^{-1} \end{pmatrix}$에 대하여 $MM' = \begin{pmatrix} A & BC^{-1} \\ O & I \end{pmatrix}$이므로 $\mathrm{det}(M) \mathrm{det}(M') = \mathrm{det}(A)$이고, 따라서 $\mathrm{det}(M) = \mathrm{det}(A) \mathrm{det}(C)$입니다.
마지막으로 행렬식의 기하적인 성질을 소개하겠습니다.
- $2 \times 2$ 행렬의 행렬식은 $$ a_{11}a_{22}-a_{12}a_{21} $$이다. $2 \times 2$ 행렬의 행렬식의 절댓값은 두 벡터 $a_1 = (a_{11}, \, a_{12})$, $a_2 = (a_{21}, a_{22})$로 만들어지는 평행사변형의 넓이와 같다.
- $3 \times 3$ 행렬의 행렬식은 $$ a_{11}a_{22}a_{33} + a_{21}a_{32}a_{13} + a_{31}a_{12}a_{23} - a_{11}a_{32}a_{23} – a_{21}a_{12}a_{33} – a_{31}a_{22}a_{13} $$이다. $3 \times 3$ 행렬의 행렬식의 절댓값은 세 벅터 $a_1=(a_{11}, \,a_{12}, \, a_{13})$, $a_1=(a_{21}, \,a_{22}, \, a_{23})$, $a_1=(a_{31}, \,a_{32}, \, a_{33})$로 만들어지는 평행육면체의 부피와 같다.
계산은 직접 해보는 것으로 하고 여기서는 $2 \times 2$ 행렬의 행렬식과 평행사변형의 넓이가 어떤 점에서 공통점이 있는지를 살펴보는 데 중점을 두겠습니다.

두 벡터 $v_1$, $v_2$로 만들어지는 평행사변형의 넓이를 $A$라 하면
- $v_1$, $v_2+cv_1$으로 만들어지는 평행사변형의 넓이는 $A$이고,
- $cv_1$, $v_2$으로 만들어지는 평행사변형의 넓이는 $cA$이고,
- $v_2$를 $u_1$과 $u_2$로 쪼개면 $A$는 $v_1$, $u_1$으로 만들어지는 평행사변형의 넓이 $A_1$과 $v_1$, $u_2$로 만들어지는 평행사변형의 넓이 $A_2$의 합 $A_1+A_2$와 같습니다. (단, $\mathrm{det}(v_1 \, u_1)$과 $\mathrm{det}(v_1 \, u_2)$의 부호가 같아야 함)
이는 행렬식의 성질과 같습니다. 이런 점에서 행렬식과 넓이가 밀접한 관계에 있는 것입니다.
이제 아래 그림과 같은 상황을 생각해볼까요?
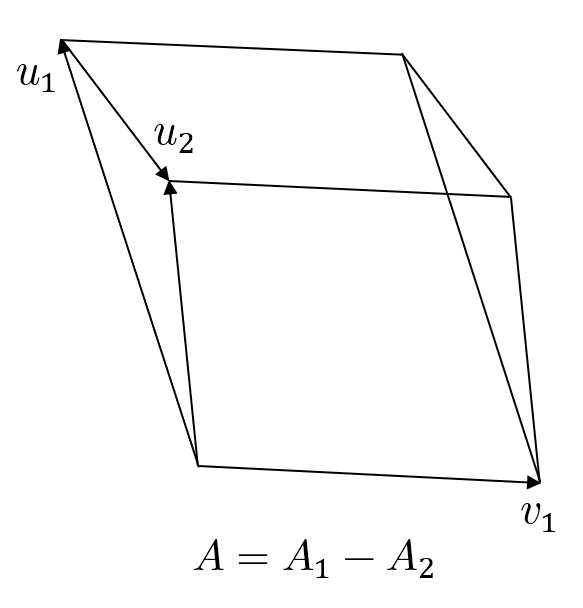
여기서는 3번 성질이 성립하지 않습니다. $A=A_1-A_2$거든요. 그렇다면 왜 이런 일이 발생하는 걸까요? 바로 "향(向)"이라는 개념 때문입니다. 오른손이 벡터 $v_1$의 종점과 $u_1$의 종점을 차례로 지나도록 감으면 엄지손가락이 화면을 뚫고 나오는 방향을 가리킵니다. 이를 + 방향이라 합니다. 반면 오른손이 벡터 $v_1$의 종점과 $u_2$의 종점을 차례로 지나도록 감으면 엄지손가락이 화면을 뚫고 들어가는 방향을 가리킵니다. 이를 - 방향이라 합니다. 이 방향의 부호는 각각 행렬식 $\mathrm{det}(v_1 \, u_1)$과 $\mathrm{det}(v_1 \, u_2)$의 부호와 같습니다.

여기서 부호를 가지는 넓이를 정의할 수 있습니다. 두 벡터가 이루는 평행사변형의 부호를 가지는 넓이는 두 벡터로 된 행렬의 행렬식과 같습니다. 이렇게 부호를 가지는 넓이를 정의하면 바로 위 그림에서 $A_2$는 음수가 되므로 비로소 $A=A_1+A_2$라고 쓸 수 있게 됩니다.
3차원 평행육면체에서도 유사한 논의를 진행할 수 있으며, 눈에 보이지 않는 4차원 이상의 도형의 부피도 행렬식을 이용하여 정의할 수 있습니다.
'교양(학문의 기초) > 공학수학' 카테고리의 다른 글
| 1. 선형대수학의 기초_(18) 대각화 가능성 (0) | 2022.08.18 |
|---|---|
| 1. 선형대수학의 기초_(17) 고윳값과 고유벡터 (0) | 2022.08.16 |
| 1. 선형대수학의 기초_(15) 행렬식 (0) | 2022.08.09 |
| 1. 선형대수학의 기초_(14) 치환 (0) | 2022.08.07 |
| 1. 선형대수학의 기초_(13) 연립일차방정식 (0) | 2022.08.07 |
