[Atkins' PHYSICAL CHEMISTRY] 1B.1(a) Pressure and molecular speed

안녕하세요! '공부는 저희 친구들이 잘해요' 블로그 작명의 모티브가 된 "수학은제친구가잘해요"입니다! 만나서 반갑습니다 ㅎㅎ

 

간단히 제 소개를 하자면, 서울대학교 화학생물공학부 21학번이고 재학중이고 현재(2022년도 2학기) 전공으로 유기화학 2, 물리화학 2, 화학생물공학기초실험을 수강하고 있습니다. 이중에서 저는 물리화학 2 내용을 연재하고자 하는데, 앳킨스 물리화학 11판 기준으로 FOCUS 16 ~ FOCUS 19 내용입니다. (International edition과 번역판과는 순서가 다르니 유의하시기 바랍니다! 제목에 쓰여 있는 TOPIC을 참고해서 내용을 봐주시면 감사하겠습니다.)

 

전반적으로 배우는 내용은 "변화"와 관련된 것으로, 분자들의 운동(FOCUS 16), 반응 속도론(FOCUS 17), 반응 동역학(FOCUS 18), 고체 표면에서의 과정(FOCUS 19)에 대한 내용을 다루게 될 것입니다. 공부하면서 같이 연재할 생각인데, 아무래도 시험 기간에는 연재하기 힘들 것 같고, 적어도 내년 겨울방학 끝나기 전까지는 연재를 끝마칠 생각입니다...!

 

이 정도로 제 소개는 마치고, 오늘 배울 내용인 기체 분자 운동론(Kinetic Molecular Theory, KMT)에 대해 같이 알아보도록 하겠습니다. 이 내용은 물리화학 1에서 다루긴 하지만, TOPIC 16A 에서 다루게 될 내용인 완전 기체의 운반 성질(Transport properties of a perfect gas)과 직접적인 연관성이 있기 때문에 이 내용을 먼저 공부하고 FOCUS 16으로 들어가는 것이 좋을 것 같아 이 내용을 먼저 다뤄보도록 하겠습니다.

이후에 물리화학 1 내용 연재하실 분께서 조금이라도 편해지셨길 바랍니다 ㅎㅎ

---

1B. 1 The model

KMT를 설명하기에 앞서, 완전 기체(perfect gas)가 무엇인지 먼저 알아보도록 하겠습니다. 많은 분들께서 완전 기체와 이상 기체(ideal gas)를 혼용하고 계실 텐데, 엄밀히 따지자면 조금 다릅니다.

이상 기체는 ① point-like mass(기체 분자의 부피는 분자 사이의 거리에 비해 매우 작기에 무시 가능&기체 분자는 질량을 가짐), ② no intermolecular force(충돌을 제외하고 분자 사이의 상호작용이 없음), ③ PV=nRT(이상 기체 방정식) 의 세 가지 조건을 만족하는 기체를 말하고, 완전 기체는 여기에 ④ const. C_v & C_p (등적 열용량과 등압 열용량이 일정) 조건까지 만족시키는 기체를 말합니다. 크게 중요한 내용은 아닙니다.

 

KMT는 기체 분자의 운동을 뉴턴 역학적인 관점에서 설명하는 이론인데, 여기에는 몇 가지 가정이 있습니다.

• 기체 분자는 충돌하기 전까지 끊임없이 무작위적인 직선 운동을 한다.
• KMT에서 설명하는 기체 분자는 완전 기체를 의미한다.
• 기체 분자 사이의 충돌이나 기체를 담고 있는 용기의 벽면과의 충돌은 모두 탄성 충돌이다(충돌 전후의 운동 에너지의 합이 항상 일정하다).

 

완전 기체는 기체 분자 자체의 부피를 무시한다고 했는데, 어떻게 기체 분자 사이 혹은 기체 분자와 용기 벽면 사이의 충돌을 설명할 수 있을까요? 이에 대해서는 뒷 내용인 "1B.2 Collisions"에서 설명하도록 하겠습니다.

 

(a) Pressure and molecular speed

결론적으로 보이고자 하는 것은 다음의 식입니다.

$$pV=\frac{1}{3}nM{v}_{rms}^2$$

여기서 $p$는 압력, $V$는 부피, $n$은 기체 분자의 몰수, $M$은 기체의 분자량, $v_{rms}$는 제곱 평균 제곱근(root-mean-square, rms) 속력입니다. $⟨⟩$가 평균을 나타내는 기호이므로 ${⟨v^2⟩}^{\frac{1}{2}}$ 로 적기도 합니다.

이를 설명하기 위해 간단한 물리학 지식(고등학교 물리학 1)이 필요한데요, 운동량과 충격량 그리고 압력입니다.

• 운동량(p)은 운동하는 물체의 질량과 속도를 곱한 값($mv$)이고, 속력이 아닌 속도를 곱하므로 운동량은 방향과 크기를 모두 가지는 벡터입니다. 운동하는 물체에 외력이 작용하지 않으면 운동량은 보존되는데, 이를 운동량 보존 법칙이라고 합니다.
• 충격량($I$)은 물체에 가해진 힘을 시간에 대해 적분한 값(${\int }_{t_1}^{t_2}Fdt$)이고, 충격량은 운동량의 변화량과 같습니다.
• 압력은 단위 면적에 가해진 힘의 크기($\frac{F}{A}$)를 의미합니다.

그럼 이제 본격적으로 위의 식을 설명해보겠습니다.

 

 저작권에 걸릴까 봐 제가 그림을 그려왔는데요, 원래 그림 못 그리니까 이해해주세요 ㅠ

일단 우리는 x 방향에 대해서만 먼저 생각해볼 것입니다. 질량이 $m$인 기체 분자가 $v_x$의 x 방향 속도로 벽을 향해 다가간다면, 벽과 충돌 후의 기체 분자의 x 방향 속도는 운동량 보존 법칙에 따라 $-v_x$이 됩니다. 따라서 운동량의 변화량의 크기는 $2m{v}_x$가 되겠네요. 그리고 위에서 설명했듯이 운동량의 변화량 = 충격량 이므로 벽이 받은 충격량은 $2m{v}_x$이 될 것입니다.

 

 

이제는 부피가 $V$인 3차원 상자에서 한 번 생각해보겠습니다. 노란색 영역의 점선 부분에 위치한 기체 분자가 $v_x$의 속도로 $\mathrm{\Delta }t$시간 동안 움직여서 면적이 $A$인 벽에 도달한다고 해봅시다. 이럴 경우 노란색으로 색칠된 부분 이외에 존재하는 기체 분자는 주어진 시간 안에 벽에 도달할 수 없을 것이고, 노란색 영역 안에 존재하는 기체 분자는 주어진 시간 안에 벽과 충돌이 "가능할 것"입니다. 즉 벽과 꼭 충돌하지 않을 수도 있다는 말인데요, 기체 분자가 왼쪽으로 움직일 수도, 오른쪽으로 움직일 수도 있기 때문이죠. 기체 분자가 무작위적인 직선 운동을 한다 했으니, 노란색 영역 안에 있는 기체 분자의 절반 정도가 벽과 충돌할 것입니다.

 

그렇다면 총 몇 개의 기체 분자가 충돌하게 될까요? 상자 안에 있는 기체 분자가 $n$몰 있다면, 기체 분자는 $n{N}_A$개 있을 것입니다($N_A$는 아보가드로 수). 기체 분자가 고르게 퍼져 있다면 노란색 영역 안에 있는 기체 분자 수는 전체 분자 수에다가 (노란색 영역의 부피)/(전체 부피)를 곱한 만큼일 것입니다. 노란색 영역의 부피는 위에 그림에도 나와 있듯이 $\left|v_x\mathrm{\Delta }t\right|A$이므로, 벽과 충돌하는 기체 분자의 수는 $$\frac{1}{2}\times n{N}_A\times \frac{\left|v_x\mathrm{\Delta }t\right|A}{V}$$입니다.

 

이제 본격적으로 압력을 구해볼 것입니다. 첫 번째 그림을 설명할 때 언급하였듯이 기체 분자 1개가 벽과 충돌할 때 벽이 받는 충격량은 $2m{v}_x$입니다. 따라서 기체 분자가 벽을 모두 때린 후 벽이 받는 총 충격량은 저 값에다가 충돌하는 기체 분자 수를 곱한

$$\frac{n{N}_{A}m{v}_x^2\mathrm{\Delta }tA}{V}$$

가 됩니다. 이때 충격량을 시간에 대해 미분하면 벽이 받는 힘을 계산할 수 있고, 힘을 작용하는 면적으로 나누면 압력이 되므로 벽이 받는 압력은 $\frac{n{N}_{A}m{v}_x^2}{V}$, $m{N}_A=M$ (분자량)이므로

$$p=\frac{nM{v}_x^2}{V}$$

가 될 것입니다.

 

이때, 온도가 동일하더라도 기체 분자의 속력이 제각각이기 때문에(이 내용은 이후 맥스웰-볼츠만 분포를 설명할 때 같이 설명하겠습니다.) x 방향 속도 $v_x$ 대신 평균값 $⟨v_x⟩$를 사용해봅시다. 또한 우리가 3차원 세상에 살고 있기 때문에 x 방향 속도만 따지기보다 3차원에서의 속력을 따지는 것이 더 나을 테니, 식을 조금만 더 고쳐봅시다. 

 

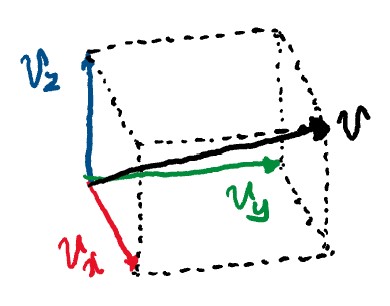
 왼쪽 그림과 같이 3차원에서의 속도 $v$는 x 방향, y 방향, z 방향 속도가 합쳐져서 나타나는 것인데, 피타고라스 정리를 사용해보면 금방 $v^2=v_x^2+v_y^2+v_z^2,⟨v^2⟩=⟨v_x^2+v_y^2+v_z^2⟩$임을 알 수 있습니다. 또한 무작위적인 운동이기 때문에 전체 분자에서 x 방향 속도의 평균, y 방향 속도의 평균, z 방향 속도의 평균이 모두 동일할 테니 $⟨v_x^2⟩=⟨v_y^2⟩=⟨v_z^2⟩$이 성립할 것입니다. 따라서 $⟨v^2⟩=3⟨v_x^2⟩,\frac{1}{3}⟨v^2⟩=⟨v_x^2⟩$이 되겠습니다.

이때 처음에 설명했던 $⟨v^2⟩=v_{rms}^2$를 이용하면 아까 구한 압력을 나타내는 식을 다시 작성하여(양변에 $V$를 곱해)

$$pV=\frac{1}{3}nM{v}_{rms}^2$$

를 얻어낼 수 있습니다.

 

수업 시간으로 따졌을 때 대략 30분 정도 수업할 분량의 내용을 다루어보았는데, 내용이 그렇게 쉽진 않지만 여러분들이 차근차근 과정을 스스로 밟아나가보시면 생각보다 쉽게 내용을 이해하실 수 있을 것입니다. 블로그 글을 처음 써보는지라 내용이 긴지 짧은지, 문체가 적당한지 아닌지 잘 모르겠네요 ㅠㅠ 여러분들의 코멘트가 블로그 글을 작성하는 데 힘이 됩니다! 도와주세요..!!

 

다음에 배울 내용은 오늘 배운 내용보다 조금 더 어렵고 분량이 많은 맥스웰-볼츠만 분포입니다. 이를 이해하기 위해서 고등학교 확률과 통계에 나오는 확률질량함수와 확률밀도함수를 어느 정도 알고 있어야 하니, 다음 글이 언제 올라올지는 모르겠지만 그때까지 공부해오시면 됩니다 ㅋㅋㅋㅋ 감사합니다!

 

다음 글 보러 가기 : https://susiljob.tistory.com/90