![[Atkins' PHYSICAL CHEMISTRY] 16B Motion in liquids](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FOvBX2%2Fbtsk1A1gPe4%2FksxGlpn5P04KxUEdfpCJn1%2Fimg.png)
안녕하세요..! 반 년도 넘어서 돌아온 수학은제친구가잘해요 입니다!! 저번 글까지 쓰고 나서 언제 쓰지 언제 쓰지 하다가 블로그의 존재를 잊고 살았네요 ㅠㅠ 일단은 9월까지 열심히 작성해서 올려보려고 해요! 근데 좀 안타깝게도 제가 물리화학 2 기말고사 범위부터 아예 버려서 FOCUS 18 부분부터는 쓰기가 좀 어려울 것 같고요... 이번 방학에는 여유롭게 FOCUS 17까지 써보는 것으로 하겠습니다! 그 이후 내용은 휴학 중에 다시 공부하면서 올리게 될 것 같고, 여기다 글 올리면서 공부한 내용 바탕으로 물리화학 2를 재수강..할 생각입니다 ㅠㅠ 공부하고 다시 하면 그래도 성적이 나쁘지 않게 나오겠죠...?
오늘 다룰 내용이 쉽지는 않은데, 그렇다고 이해가 불가능하게 어렵지도 않아요! 식이 너무 많이 나와서 머리에 한 번에 안 들어오실 수 있는데, 마음의 여유를 가지고 과정을 따라가다 보면 '오 생각보다 내용이 많지는 않구나' 생각이 드실 것입니다! 두 번으로 나눠서 글 올린다고 했는데, 그냥 한 번에 올려도 될 것 같아서 쭉 다뤄볼게요. 오랜만이지만 다시 한 번 열심히 달려보겠습니다! 아 그리고 그림 그리는 게 생각보다 많이 빡세서 이제는 그냥 책에 있는 그림 그냥 가져오려고요... 돈 벌려고 하는 거 아니니까 괜찮겠죠 뭐 ㅋㅋㅋ
이전 게시글 목록입니다.
- https://susiljob.tistory.com/89 (1B.1(a) Pressure and molecular speed)
- https://susiljob.tistory.com/90 (1B.1(b) The Maxwell-Boltzmann distribution of speed)
- https://susiljob.tistory.com/93 (1B.1(c) Mean values & 1B.2 Collisions)
- https://susiljob.tistory.com/95 (16A.1 The phenomenological equations (+ collision flux))
- https://susiljob.tistory.com/97 (16A.2 The transport parameters)
16B Motion in liquids
오늘 다룰 내용은 액체 안의 입자들이 어떻게 움직이는지에 관한 내용입니다. 정말 많은 화학 반응이 액체 안에서 진행되기 때문에 여러 가지 액체의 특성을 파악하는 것은 다양한 화학 반응을 이해하는 것에 매우 큰 도움을 주죠. 이를 위해 액체의 특성에 대해 다양한 방법으로 파악하는데, NMR(Nuclear Magnetic Resonance)을 이용하거나 INS(Inelastic Neutron Scattering)를 이용하는 방법이 있습니다. NMR은 유기화학 시간에 들어보셨을 텐데, 자기장 안에 물질을 놓고 뭔가 공명을 만들어 분석하는 거죠(자세한 건 유기화학 책을 참고해주세요..ㅎ). INS는 중성자를 물질에 쏜 다음 잃거나 얻은 에너지를 분석하여 뭔가를 알아내는 거라고 해요.
16B.1 Experimental results
고전적인 방법으로는 특정 기구를 이용해서 액체의 점성(viscosity)을 측정하는 방법, 액체 속에 이온을 넣고 전기장을 걸어주었을 때 이온의 움직임을 분석하는 방법이 있습니다.
(a) Liquid viscosity
먼저 액체의 점성입니다! 제가 저번 글에서 기체는 분자 사이의 충돌을 통해서 운동량을 전달한다고 말씀드렸는데요, 액체는 주변 분자와의 상호 작용을 통해서 운동량을 전달한답니다. 따라서 기체와 다르게 온도가 높아지면 주변 분자의 상호 작용을 벗어나는 분자가 많아지게 되어 운동량 전달이 더 어려워지게 됩니다. 주변 분자의 상호 작용을 벗어나기 위한 에너지를 $ E_{a} $ 라 하면(다들 아시는 활성화 에너지 맞아요!) 볼츠만 분포에 따라 이 에너지 이상의 에너지를 가지는 분자 수는 $ e^{-\frac{E_{a}}{RT}} $ 에 비례하겠죠. 근데 얘네가 적을수록 운동량을 잘 전달하게 되는 것이니 액체의 점성을 간단하게 다음의 식으로 적을 수 있겠습니다.$ E_{a} $ 앞에 부호가 +로 바뀐 것을 확인해주세요!
$$ \eta =\eta _{0} e^{\frac{E_{a}}{RT}} $$
근데 사실 이 식은 문제가 좀 있는데, 보통 액체의 점성은 밀도에도 영향을 받는다고 해요. 다들 아시다시피 밀도 또한 온도에 따라 달라지기 때문에 단순히 저 위의 식을 적용해서 점성을 구하는 것은 조금 힘들답니다 ㅠ 그리고 $ E_{a} $ 의 값을 구하는 것도 매우 어려워서 사실 크게 쓸모있는 식인지는.... 잘 모르겠습니다...
(b) Electrolyte solutions
이제 여기서부터는 이온의 움직임을 알아보겠습니다. 일단 여기서는 이온 각각의 움직임보다 이온이 녹아 있는 전해질 용액에 대해서 먼저 알아보려고 해요. 가장 먼저 알아볼 개념은 컨덕턴스(conductance)입니다. 저항의 역수로, 전기가 얼마나 잘 통하는지 알려주는 값입니다.
저항을 R, 전류를 I, 전위차를 $ \Delta \mathit{\Phi} $ 라 했을 때 옴의 법칙에 의해 $ R =\frac{\Delta \mathit{\Phi}}{I} $ 가 성립하며, 단위는 $ \Omega =\frac{\textup{V}}{\textup{A}} $ 을 쓰니까
컨덕턴스를 G라 하면 $ G = \frac{I}{\Delta \mathit{\Phi }} $ 이고, 단위는 S(Siemens 지멘스) ($ S =\frac{\textup{A}}{\textup{V}} $)를 사용합니다. 또한 도선의 단면적이 클수록, 도선이 짧을수록 전류 이동이 수월하기 때문에 비례 상수를 붙여서 $ G =\kappa \frac{\mathit{A}}{l} $이라고 할 수 있습니다. (A가 단면적, l이 길이)
여기서 $ \kappa $ 를 conductivity라 하는데요, 이 값이 클수록 전류가 잘 흐른다는 뜻이겠죠? 우리가 지금 전해질 용액에 대해서 생각하고 있으니까 넣어준 전해질의 농도에 따라 전류가 흐르는 정도가 달라져 conductivity가 달라지게 될 거예요. 따라서 또 다시 비례 상수를 가지고 와서, 넣어준 전해질의 농도를 c라 하면 $ \kappa = \Lambda_{m} c $ 이라고 할 수 있을 겁니다.
또 여기서 $ \Lambda_{m} $를 molar conductivty라 하는데, 안타깝게도(?) 이 값이 농도에 따라 달라지는 값이랍니다 ㅠ 만약 약한 전해질을 조금 넣어주었을 경우에는 전해질이 이온으로 해리되는 비율이 매우 낮아 conductivity가 농도에 비례하지 않게 되고요, 강한 전해질을 많이 넣어주었을 경우에는 이온 간의 상호 작용이 강해져 이 또한 conductivity가 농도에 비례하지 않게 돼요. 그래서 Friedrich Kohlrausch라는 분께서 Kohlrausch law라는 것을 만들어냈는데, 그 식은 다음과 같습니다.
$$ \Lambda_{m} = \Lambda_{m}^{\circ} - Kc^{\frac{1}{2}} $$
여기서 $ \Lambda_{m}^{\circ} $를 limiting molar conductivity라 하는데, 전해질 농도가 0에 가까울 때의 molar conductivity 값이라고 보면 됩니다. 얘 같은 경우에는 이온 사이에 상호 작용이 없다고 가정하고 이온별로 conductivity를 생각해서 더하면 될 것 같죠? 따라서 다음의 식을 생각해볼 수 있습니다.
$$ \Lambda_{m}^{\circ} = \lambda_{+} \nu_{+} + \lambda_{-} \nu_{-} $$
$ \lambda $는 각 양이온과 음이온의 limiting molar conductivity이고요, $ \nu $는 대충 이런 식입니다. MgCl2가 Mg2+ 한 개와 Cl- 두 개로 해리되잖아요? 그러면 $ \nu_{+} = 1 $이고 $ \nu_{-} = 2 $랍니다.
사실 여기까지 어려운 내용은 딱히 없었는데, 바로 위 내용이 식이 좀 많았죠? 이쯤에서 잠깐 멈추고 무슨 식이 나왔었는지 잠깐 생각하시고 다음 내용 보시길 바라요!
16B.2 The mobilities of ions
(a) The drift speed
지구에서 공기 저항 없이 자유 낙하하는 물체는 1초에 9.8m/s씩 계속해서 속력이 증가하죠. 그치만 공기 저항이 있는 경우는 달라요! 속력이 증가하는 속도가 더 느릴 뿐더러 일정 시간이 지나면 더 이상 속력이 증가하지 않는 것처럼 보이기도 해요. 여기서 다루는 drift speed도 이와 비슷한 개념입니다. 전해질 용액에 전기장을 걸어줄 때 이온이 움직이는 종단 속력을 drift speed라 합니다.
왼쪽 그림은 저희 교수님 강의 자료에 있는 그림인데요, 전해질 용액에 l만큼 떨어지게 왼쪽에는 + 전극을, 오른쪽에는 - 전극을 꽂고 $ \Delta \mathit{\Phi} $만큼의 전위차를 걸어준 상황입니다. 그러면 그림의 양전하를 띤 이온은 정전기적 인력을 받아 오른쪽으로 움직이는데, 용매의 점성에 의해 이 움직임을 방해하는 마찰력이 왼쪽으로 가해질 거예요. 정전기적 인력과 마찰력이 서로 평형을 이룰 때의 이온의 속력이 drift speed가 되겠죠?
정전기적 인력을 $ \textup{F}_{electric} $이라 하면 $ \textup{F}_{electric} = qE $입니다. (q는 전하량, E는 전기장의 세기) 이 식은 일반물리학에 나오는 식이니, 이해가 안 되시면 일반물리학 책을 참고해주세요! 여기서 $ z $를 이온의 전하량(Ca2+면 2, OH-면 1)이라 하면 $ q=ze $이므로(e는 전자 하나의 전하량, 1.60*10^(-19)C), $ \textup{F}_{electric} = zeE $가 되겠습니다.
이번에는 마찰력을 생각해보겠습니다! 마찰력을 $ \textup{F}_{viscous} $ 이라 하면 $ \textup{F}_{viscous} = fs $ 가 성립해요. 여기서 f가 마찰 계수, s가 이온의 속력입니다. 아까 이 두 힘이 평형을 이룰 때 이온의 속력이 drift speed라 했으니, $zeE = fs$인 s가 drift speed겠죠? 따라서 drift speed는 다음의 식으로 구할 수 있습니다.
$$ s = \frac{zeE}{f} $$
여기서 이온이 같은 세기의 전기장 안에서 얼마나 잘 움직이는지 알아보려면 $ u = \frac{ze}{f} $를 생각해보면 될 것 같아요. u를 mobility of ion이라 하는데, 이 값이 클수록 같은 전기장 세기일 때 이온이 더 빠르게 움직일 수 있겠죠.
u에서 바로 알 수 없는 값이 마찰 계수죠? 구체의 입자가 점성을 가진 유체를 이동할 때 마찰 계수는 Stokes' law를 따른다고 하는데 그 식은 $ f = 6 \pi \eta a $입니다. 여기서 a가 좀 특이한데, 단순히 입자의 반지름을 말하는 것이 아니라 수화됐을 때 그 입자에 묶여있는 물 분자까지 포함하는 구의 반지름입니다. 이를 hydrodynamic radius 또는 Stokes radius라고 합니다. 같은 전하량이면 크기가 작은 이온 주변에 더 많은 물 분자가 묶이게 돼서 크기가 작을수록 a가 커지는 경향성이 있어요. 따라서 같은 전하량이면 크기가 작은 이온이 u가 더 작아 더 느리게 움직이게 된답니다. 밑의 표는 책에 나와 있는 몇몇 이온에 대한 u값인데, 앞서 설명한 경향성을 보실 수 있어요.
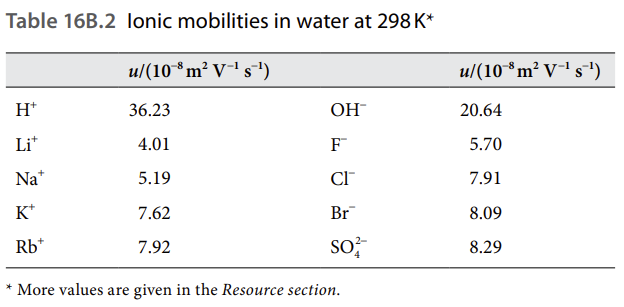
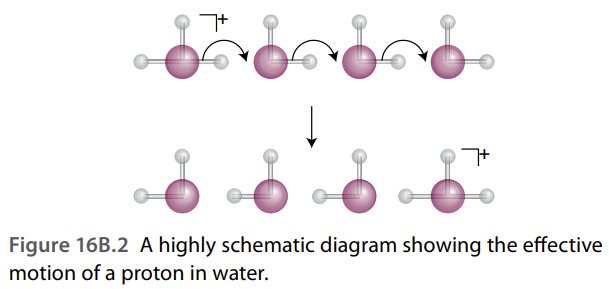
여기서 H+랑 OH-가 다른 것들에 비해 특이하게 u값이 매우 높은데요, 대애충 설명하자면 물 안에서의 mobility라서 그렇다고 보면 될 것 같아요. H+의 u값은 Grotthuss Mechanism으로 설명하는데요, 저 양성자가 물 분자의 방해를 뚫고 이동하는 게 아니라, 물 분자에 붙어서 닌자처럼(??) 이동하기 때문에 더 빠르게 이동할 수 있다고 합니다. 다시 말하자면, 양성자가 물 분자 중 하나를 하이드로늄 이온(H3O+)으로 만들고, 이 이온이 주변의 물 분자에 양성자를 빠르게 전달하여 하이드로늄 이온으로 만드는 식이죠. 왼쪽 그림을 통해서 이해하시면 될 것 같아요. 근데 이 메커니즘은 설명하는 방법 중 하나이고, 실제 메커니즘이 어떻게 되는지는 잘 모른다고 해요.
(b) Mobility and conductivity
여기서는 이제 mobility of ion(u)과 limiting molar conductivity of ion($ \lambda $)을 엮어보려 해요! 일단 가장 먼저 16B.1(b)에서 나왔던 식을 싹 합쳐볼게요. 한 가지 종류의 전하를 가진 되게 적은 수의 이온에 대해서 생각할 거라서 Kohlrausch law까지 갈 것 없이 molar conductivity만 따지면 $ \lambda $라고 할 수 있겠습니다.
$$ \lambda = \frac{\kappa}{\nu c} = \frac{Gl}{A \nu c} = \frac{Il}{\Delta \mathit{\Phi} A \nu c} $$
만약 전해질을 c몰 넣었고, 전해질 한 입자 당 $ \nu $개로 이온이 해리되어 나온다면 이온 몰수는 $ \nu c $가 되겠죠.
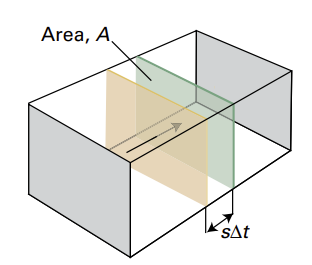
여기서 이제 전류 I에 대해서만 다시 잘 나타내볼게요. 전류라는 것이 단위 시간당 도선의 한 단면적을 지나는 전하량이니, 일정 시간 동안 가상의 단면적을 지나가는 이온의 수를 구하면 될 것 같네요. $ \Delta t $동안 지나가는 이온의 수는 왼쪽 그림의 노란색 벽과 초록색 벽 사이에 존재하는 이온의 수와 같습니다(앞에서 이런 거 많이 했었죠?). 전체 부피가 V이고 전체 전해질 몰수가 n이라 하고, 용기 전체에 고르게 이온이 퍼져 있다고 가정하면 저기 두 개의 벽 사이에 존재하는 이온의 수는 $ \frac{As \Delta t}{V} \times \nu nN_{A} $입니다. 이온 한 개의 전하량이 $ ze $이므로 전류는 다음과 같이 구할 수 있겠습니다.
$$ I = \frac{As \Delta t}{V} \times \nu nN_{A} \times ze \div \Delta t = zsA \nu \frac{n}{V} eN_{A} = zsA \nu cF $$
여기서 F는 전자 1몰의 전하량을 나타내는 패러데이 상수입니다. 이제 저 위에 $ \lambda $에 대한 식과 바로 위에 있는 전류를 합쳐보면 이렇게 되겠네요!
$$ \lambda = \frac{zsA \nu cF l}{\Delta \mathit{\Phi} A \nu c} = zF \times \frac{l}{\Delta \mathit{\Phi}} \times s = zF \times \frac{1}{E} \times uE = zuF $$
전기장의 세기는 $ E = \frac{\Delta \mathit{\Phi}}{I} $이고 아까 위에서 $ s = uE $ 라고 정의했었죠. 식이 뭔가 되게 복잡했는데 결국 도출되는 식은 좀 간단해 보이죠? 아까 전에 나왔던 $ \Lambda_{m}^{\circ} = \lambda_{+} \nu_{+} + \lambda_{-} \nu_{-} $ 여기에 위에서 구한 식을 대입하면 $ \Lambda_{m}^{\circ} = (z_{+} u_{+} \nu_{+} + z_{-} u_{-} \nu_{-})F $가 되겠습니다.
(c) The Einstein relations
자 이제 마지막입니다! 우리가 다음 글에서 배울 식 중에 $ s = \frac{D\textbf{F}}{RT} $ 가 있는데요(저 F가 자꾸 반복되어 적당한 폰트 찾는게 어려워서 그냥 저걸로 해봤어요 ㅠ), D는 우리가 저번에 배운 diffusivity고 F는 아직 모르셔도 돼요. 근데 이 F가 $ \textbf{F} = zFE $(뒤쪽 F는 패러데이 상수)로 구할 수 있다고 하네요. 그래서 $ u = \frac{zDF}{RT} $가 성립하는데, 이를 Einstein relation이라고 합니다. 당연히 D가 커지면 u도 커질 텐데, 그러면 T와 u는 반비례하냐? 뭔가 이상하죠. 저번 시간에 D가 T의 3/2제곱에 비례한다 했으니 u는 T의 제곱근에 비례할 것이고 결국 온도가 증가하면 mobility가 증가하게 됩니다.
그리고 저 u에 대한 식을 바로 위에 $ \Lambda_{m}^{\circ} $ 구하는 식에 넣어보면 $ \Lambda_{m}^{\circ} = (\nu_{+} z_{+}^{2} D_{+} + \nu_{-} z_{-}^{2} D_{-}) \frac{F^{2}}{RT} $ 로 나타낼 수 있겠죠? 이 식을 Nernst-Einstein equation이라고 합니다.
자, 이것으로 오늘 내용을 마쳤습니다. 어떠셨나요? 제가 여기 부분 공부하면서 느낀 점이 식이 너무 많다는 것이었습니다 ㅠ 사실 하나하나 놓고 보면 그러려니 하겠는데, 이 식 저 식 서로 합치고 하나로 만들고 하는 과정이 좀 어렵다고 생각했어요... 하지만 이쪽 부분은 저번 글처럼 테일러 급수 같이 좀 어려운 수학 안 쓰고 그냥 정리만 잘 하면 좀 더 쉽게 유도할 수 있었던 것 같아요! 시험 닥쳐서 한 번에 다 외우려 하면 머리에 안 들어오고 초조해지니까 좀 여유 있을 때 많이 보면서 익숙해지는 게 훨씬 도움이 될 것 같다는 생각입니다(미래에 재수강할 저에게 하는 말입니다).
이제 다음 글부터 다룰 내용은 diffusion, 확산과 관련한 내용이긴 한데요... 좀 많이 어려워요... 물리화학 2에서 배우는 FOCUS 16부터 FOCUS 19까지의 내용을 어려운 순서대로 줄 세워보라고 하면 거의 가장 앞에 있는 수준이지 않나 싶어요. TOPIC 16C는 분량 욕심 안 부리고, 하루에 이해하기 좋은 만큼만 딱 다뤄보겠습니다! 지금 생각으로는 세 번에 나눠서 내용을 다룰 것 같습니다. 다음 글은 7월 되기 전에 써서 올리겠습니다. 감사합니다!!
다음 글 보러 가기 : https://susiljob.tistory.com/125