![[Atkins' PHYSICAL CHEMISTRY] 16A.1 The phenomenological equations (+ collision flux)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fmmg4n%2FbtrPtvvD5L0%2FoR5qxrMfjxvPwHMfyLrbPk%2Fimg.jpg)
안녕하세요! 수학은제친구가잘해요입니다 ㅎㅎ 아직 시험은 끝나기 전이지만, 조금씩 써서 올리려고 해요! 지금 처음 글쓰는 날짜는 10월 21일 새벽이고요, 아마 글 올라가는 시점은 다음 주 정도로 예상하고 있습니다. 오늘은 간단하게만 쓰고 넘어가려고요 ㅎㅎ
이제 본격적으로 우리 학부의 물리화학 2 내용이 시작될 것입니다. TOPIC 16A의 제목은 "Transport properties of a perfect gas"인데요, "Flux"와 여러 가지 flux에 대한 상수에 대한 내용입니다. 이번 글에서는 Flux가 무엇인지, 우리가 다룰 Flux는 어떤 종류가 있는지, 그리고 collision flux가 무엇인지 다룰 것입니다. 내용상으론 collision flux 내용을 다음 글로 넘기는 게 진행이 더 매끄럽겠지만, 다음 글 내용이 너무 많고 어려워질 것 같아서 이번 글에서 다루도록 하겠습니다.
이전 게시글 목록입니다.
- https://susiljob.tistory.com/89 (1B.1(a) Pressure and molecular speed)
- https://susiljob.tistory.com/90 (1B.1(b) The Maxwell-Boltzmann distribution of speed)
- https://susiljob.tistory.com/93 (1B.1(c) Mean values & 1B.2 Collisions)
16A.1 The phenomenological equation
현상학적 방정식(phenomenological equation)이란 현상에 대한 관찰을 바탕으로 만들어낸 방정식입니다. 즉, 분자들의 특성 등에 대한 이해를 제외하고 현상에 대한 관찰을 증거로 삼아 만든 방정식인데요, 우리가 다룰 flux에 대한 방정식도 현상학적 방정식의 한 종류입니다.
그렇다면 flux는 뭘까요? 물리화학에서 정의하는 flux는 단위 시간동안 단위 면적을 지나는 알짜 양이라고 할 수 있겠습니다. 간단하게 수식으로 작성하면 $ flux = \frac{amount}{area\times time} $가 되겠습니다. 기호는 J를 사용할 것이고요, 우리는 matter flux, energy flux, momentum flux에 대해서 다뤄볼 것입니다.
1. Matter flux
먼저 matter flux인데요, 기체 분자들이 이동하는 것에 대한 flux라고 생각하시면 됩니다. matter flux는 기체 분자의 질량이 이동하는 것(mass flux), 1몰을 기준으로 기체 분자가 이동하는 것(mole flux), 또는 한 개를 기준으로 기체 분자가 이동하는 것(molecular flux)으로 생각해볼 수 있습니다. 이걸 전부 다 제대로 알고 넘어가실 필요는 없고, 일단 이런 게 있다 정도만 알고 넘어가셔도 좋습니다. 다 비슷비슷하니까 molecular flux에 대해서만 설명하고 넘어갈 거고요, 나머지는 독자에게 맡기...는 건 아니고 안 하셔도 상관 없어요 ㅋㅋㅋ
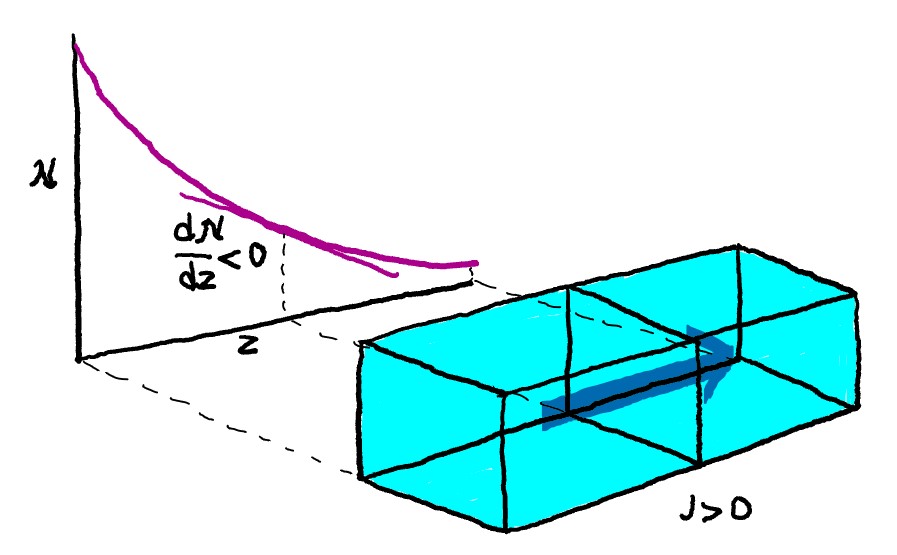
왼쪽 그림은 하늘색 상자와 상자 안 기체 분자들의 z 방향에 따른 number density를 나타낸 그래프입니다. '경험적으로' number density($ \rho _{N} $)가 큰 쪽에서 작은 쪽으로 기체 분자들이 이동한다는 사실을 알고 있죠? 그리고 농도 기울기에 따라 이동하는 양이 달라진다는 것도 알고 있습니다. 따라서 다음의 관계가 성립함을 알 수 있습니다.
$$ J_{matter} \propto \frac{\mathrm{d} \rho _{N}}{\mathrm{d} z} $$
이때 옆에 그림에서도 알 수 있듯이, z 값이 커짐에 따라 number density가 줄어든다면 $ \frac{\mathrm{d} \rho _{N}}{\mathrm{d} z} $는 음수겠지만, 전체적으로 기체 분자는 z 방향으로 이동할 테니 flux는 양수일 것입니다. 따라서 양수값을 가지는 비례 상수를 도입하면 다음의 식을 얻어낼 수 있어요.
$$ J_{matter} = -D \frac{\mathrm{d} \rho _{N}}{\mathrm{d} z} $$
이 식을 Fick's first law in terms of the diffusion coefficient 혹은 Fick's first law of diffusion이라고 합니다. 이때 $ D $를 diffusion coefficient라고 하는데, 간단히 diffusivity라고도 합니다. 이 값이 클수록 단위 시간당 단위 면적을 지나는 기체 분자의 양이 커지는 것이므로, 기체의 확산 정도가 크다고 생각할 수 있습니다.
diffusivity의 단위를 한 번 생각해봅시다. 좌변의 단위는 1/(area)(time) = $ \textup{m}^{-2} \cdot \textup{s}^{-1} $이고, 우변에 $ \frac{\mathrm{d} \rho _{N}}{\mathrm{d} z} $의 단위는 number density(1/volume)을 길이로 나누는 값이므로 $ \textup{m}^{-4} $이죠? 따라서 diffusivity의 단위는 $ \textup{m}^{2} \cdot \textup{s}^{-1} $가 되겠습니다.
아까 전에 matter flux는 세 종류로 나뉠 수 있다 하였는데, 전부 위와 같은 방식으로 구할 수 있고 비례 상수는 모두 diffusivity로 나타냅니다. diffusivity의 단위는 일정하고, 따라서 mass flux는 $ J_{matter}=-D\frac{\mathrm{d} \rho }{\mathrm{d} x} $, molar flux는 $ J_{matter}=-D\frac{\mathrm{d} c}{\mathrm{d} x} $로 나타냅니다. ($ \rho $는 밀도, $ c $는 몰 농도입니다.) 어렵지 않으니 굳이 부연설명은 덧붙이지 않도록 하겠습니다.
2. energy flux
energy flux는 matter flux와 같은 방식으로 생각하면 됩니다. 이번에는 기체 분자의 농도 기울기 대신 온도 기울기를 생각해보면 되는데, 온도가 높은 곳에서 낮은 곳으로 열이 이동하기 때문입니다. 이 또한 온도 기울기와 energy flux의 부호가 서로 다를 테니 양수값을 가지는 비례 상수를 도입하여 다음의 식을 얻어낼 수 있습니다.
$$ J_{energy}=-\kappa \frac{\mathrm{d} T}{\mathrm{d} z} $$
이 식을 Fourier's law of heat conduction라고 하며, 비례 상수 $ \kappa $는 coefficient of thermal conductivity 또는 간단히 thermal conductivity, heat conductivity라고 합니다. 이 상수 값이 클수록 온도 전달이 더 효율적으로 되겠네요. 이 식은 열 전도에 의한 에너지 이동을 표현한 식이고요, 다른 방식에 의한 에너지 이동은 책에서 다루지 않습니다.
$ \kappa $의 단위만 보고 바로 넘어갑시다. 에너지의 단위는 J(줄)이므로 좌변의 단위는 $ \textup{J} \cdot \textup{m}^{-2} \cdot \textup{s}^{-1} $ 이고, 우변의 $ \frac{\mathrm{d} T}{\mathrm{d} z} $ 단위는 $ \textup{K} \cdot \textup{m}^{-1} $입니다. 따라서 $ \kappa $의 단위는 $ \textup{J} \cdot \textup{K}^{-1} \cdot \textup{m}^{-1}\cdot \textup{s}^{-1} $입니다. 이때 $ \textup{J} \cdot \textup{s}^{-1}=\textup{W} $ 이므로 $ \textup{W} \cdot \textup{K}^{-1} \cdot \textup{m}^{-1} $로 나타내기도 합니다.
3. momentum flux
momentum flux는 앞에 두 개보다 조금 더 이해하기 어려웠는데요, 이런 상황을 한 번 생각해봅시다. 물이 움직이지 않는 잔잔한 호수가 있습니다. 그 위로 바람이 한 번 휙 하고 불면 호수 표면의 물이 바람이 불어온 방향대로 움직일 것입니다. 근데 완전 표면에 있는 물만 움직이는 것은 아니고, 표면 밑에 물도 그 방향대로 움직이기는 하겠지만 조금 느리게 움직일 것입니다. 이때 물의 움직임이 전달되는 방향은 물이 움직이는 방향과 수직이겠네요. 이런 느낌으로 이해하시면 되고요, 그림을 통해 조금 더 설명해보겠습니다.
서로 평행한 두 판 사이에 유체가 채워져 있고, 빨간 화살표는 x 방향 속도를 나타낸 것입니다. 제가 조금 전에 예시를 든 것과 비슷한 상황인데요, 바람이 불어오는 쪽이 z=0 부분이고 z 방향을 따라서 x 방향 속도가 전달되고 있습니다. 왼쪽 그림에서 z 방향에 따른 x 방향 속도의 변화량이 일정한데, 이러한 유체를 뉴턴 유체(Newtonian fluid)라고 합니다. 뉴턴 유체가 무엇인지 더 알아보진 않을 거고, 이 블로그에 누군가가 유체 역학 내용을 연재하면 그때 그 글을 보는 것으로 하죠 ㅎㅎ
따라서 momentum flux는 다음의 식으로 나타낼 수 있겠습니다.
$$ J_{momentum} = -\eta \frac{\mathrm{d} v_{x}}{\mathrm{d} z} $$
이 식을 Newton's law of viscosity라 하며, $ \eta $를 coefficient of viscosity 또는 간단히 viscosity라 합니다. viscosity는 우리말로 점성입니다. 즉 끈적끈적한 정도를 나타낸 것인데, 위 식에 의하면 유체가 끈적끈적할수록 운동량을 더 잘 전달할 수 있다는 뜻이 되겠습니다. viscosity의 단위는 위와 같은 방식으로 구하면 $ \textup{kg}\cdot \textup{m}^{-1}\cdot \textup{s}^{-1} $인데, $ \textup{Pa}= \frac{\textup{N}}{\textup{m}^2} $임을 이용하면 $ \textup{Pa}\cdot \textup{s} $입니다. viscosity는 cgs unit인 P(poise, 푸아즈)로 나타내기도 하는데, $ 1\textup{Pa}\cdot \textup{s}=10\textup{P} $입니다.
책에는 나와 있지 않지만 수업 시간에 간단히 배운 내용 하나를 설명해볼 텐데요, momentum flux는 '힘/면적'의 단위를 가지는 '응력(stress)'과 관련이 있다는 내용입니다. 응력은 압력과 단위는 같지만 그 개념이 매우 다른데요, 압력은 외부에서 누르는 단위 면적당 힘이라면 응력은 물체가 외부 힘을 견뎌내는 단위 면적당 힘을 의미합니다. 응력에는 다양한 종류가 있는데, momentum flux는 그중 전단 응력(shear stress)과 관련이 있습니다. 전단 응력은 물체 내부 단면적에 대해 힘이 평행한 방향으로 작용할 때 발생하는 응력인데, 아까 잔잔한 호수에 부는 바람이 여기서 말하는 힘과 같은 역할을 한다고 보면 되겠습니다. 결론적으로, momentum flux는 전단 응력과 같다고 물리적으로 해석할 수 있습니다.
(저도 딱 이 정도까지만 배워서 그 너머에 어떤 내용이 있는지는 잘 모르고요 ㅠ 결론만 알아두셔도 될 것 같습니다!)
여기까지 배운 내용을 요약하면 다음과 같습니다:
- Flux는 단위 시간당 단위 면적을 이동하는 양을 말하고, 그 종류에는 matter flux, energy flux, momentum flux가 있습니다. 기호는 J를 사용합니다.
- $ J_{matter} = -D \frac{\mathrm{d} \rho _{N}}{\mathrm{d} z} $이고, $ D $를 diffusion coefficient 또는 diffusivity라 합니다. diffusivity의 단위는 $ \textup{m}^{2} \cdot \textup{s}^{-1} $입니다.
- $ J_{energy}=-\kappa \frac{\mathrm{d} T}{\mathrm{d} z} $이고, $ \kappa $를 coefficient of thermal conductivity 또는 thermal conductivity라 합니다. thermal conductivity의 단위는 $ \textup{J} \cdot \textup{K}^{-1} \cdot \textup{m}^{-1}\cdot \textup{s}^{-1} = \textup{W} \cdot \textup{K}^{-1} \cdot \textup{m}^{-1} $입니다.
- $ J_{momentum} = -\eta \frac{\mathrm{d} v_{x}}{\mathrm{d} z} $이고, $ \eta $를 coefficient of viscosity 또는 viscosity라 합니다. viscosity의 단위는 $ \textup{kg}\cdot \textup{m}^{-1}\cdot \textup{s}^{-1} = \textup{Pa}\cdot \textup{s} $ 또는 P(푸아즈)입니다. 1 Pa·s = 10P입니다.
4. effusion
effusion은 우리말로 '분출'인데요, 좁은 공간을 유체가 통과하는 것을 분출이라 하죠. 이건 엄밀히 말해 transport property는 아니지만 diffusion과 밀접한 관련이 있다고 합니다. 분출 속도와 관련한 현상학적 방정식은 Graham's law of effusion인데, 기체의 분출 속도는 기체의 분자량의 제곱근 값에 반비례한다는 법칙입니다. 예를 들어 분자량이 각각 10, 40인 기체 분자 A와 B가 있다고 할 때, A의 분출 속도가 B의 분출 속도의 2배가 된다는 것입니다. 분출은 이 정도만 설명하고 넘어가겠습니다.
16A.2 The transport parameters
이제 각 flux에 대한 비례상수를 구해볼 건데, 이번 글에서는 다루지 않을 것이고 이를 구하는 데 필요한 collision flux에 대해서만 설명하도록 하겠습니다. collision flux는 단위 시간당 단위 면적에 충돌하는 횟수를 나타낸 것인데, 이를 구하기 위해서는 제가 전에 설명한 TOPIC 1B의 내용에 대해 알고 계셔야 합니다. 글 처음에 올려놓은 이전 게시글 목록에서 내용을 확인하시기 바랍니다!
collision flux는 $ Z_W $ 로 나타내고, 결론부터 제시하면 다음과 같습니다.
$$ Z_W = \frac{p}{(2\pi mk_{B}T)^{\frac{1}{2}}} = \frac{pN_{A}}{(2\pi MRT)^{\frac{1}{2}}} = \frac{1}{4}\rho _{N}\left< v\right> $$
collision flux에서 말하는 collision은 분자 사이의 충돌이라기보다, 기체 분자를 담는 용기의 벽면 혹은 임의의(가상의) 평면에 충돌하는 것을 말합니다.
왼쪽 그림과 비슷한 그림을 첫 글에서도 한 번 보셨을 텐데요, 설명을 하자면 (2차원으로 그려놨지만) 3차원 상자 안에 +x 방향에 수직인 상자 안쪽 벽을 기체 분자가 때리는 상황입니다. Mean values 설명할 때 설명했듯이, 확률밀도함수 $ f(x) $에서 $ x $의 평균은 $ \left< x\right>=\int_{-\infty }^{\infty }xf(x)dx $입니다. 따라서, + x 방향 속도의 평균을 구하면 $ \left< v_x^+\right>=\int_{0}^{\infty }v_xf(v_x)dx $ 입니다. 우리는 +x 방향 속도가 양수인 것만 다룰 생각입니다.
여기서 맥스웰-볼츠만 분포에서 설명한 내용이 나오는데요, x 방향 속도에 따른 분자의 분포 식을 가져와보겠습니다.
$$ f(v_x)=K_x e^{-\frac{mv_x^2}{2k_{B}T}}, K_x = (\frac{m}{2\pi k_{B}T})^\frac{1}{2} $$
이를 이용해서 +x 방향 속도를 구하면 $ \left< v_x^+\right> = ({\frac{k_{B}T}{2\pi m}})^{\frac{1}{2}} $ 가 됩니다. 적분 과정은 생략하도록 하겠습니다.
이제 벽을 때리는 분자의 수, 곧 충돌 횟수를 구해보겠습니다. 제가 저기에 연두색으로 칠해놓은 부분 안의 분자들이 옆에 벽을 때릴 수 있겠죠? 따라서 저 부분의 부피에 number density를 곱해주면 충돌 횟수가 나오게 됩니다.
$$ (number \ of \ collision)=\rho_N A \left< v_x^+\right>\Delta t $$
여기서 헷갈리는데, 저 안에 - x 방향으로도 움직이는 분자가 있을 수 있는 것 아니냐, 저기서 구한 값의 절반만 때리는 거 아니냐 하는 의문이 들 수 있겠는데요. 이미 우리는 + x 방향으로만 움직이는 분자만 고려하기로 했습니다. 제가 <> 안에 + 기호를 위 첨자로 달아둔 이유이기도 하고요, 아까 적분할 때도 0부터 적분을 시작했죠? 헷갈리지 않도록 주의해야겠습니다 ㅎㅎ
이제 collision flux를 한 번 구해봅시다! 충돌 횟수를 면적과 시간으로 나눠주면 되는데, 그냥 쉽게 $ A $와 $ \Delta t $를 없애주면 되죠? number density는 $ \rho_{N} = \frac{p}{k_{B}T} $임을 저번 글에서 구했으니 이것까지 대입해서 구해보죠.
$$ Z_{W} = \rho_{N} \left< v_x^+ \right> = \frac{p}{k_{B}T} ({\frac{k_{B}T}{2\pi m}})^{\frac{1}{2}} = \frac{p}{(2\pi mk_{B}T)^{\frac{1}{2}}} $$
여기서 분모, 분자에 아보가드로 수를 각각 곱해주면 처음에 설명했던 두 번째 식이 나오게 될 것이고요. 우리가 또 저번 글에서 $ \left< v\right>=(\frac{8RT}{\pi M})^{\frac{1}{2}}=(\frac{8k_{B}T}{\pi m})^{\frac{1}{2}} $임을 구했으니 $ \left< v_x^+\right>=\frac{1}{4}\left< v\right> $임을 알 수 있고, 이를 대입하면 마지막 식도 구해질 것입니다.
자, 이렇게 해서 TOPIC 16A의 앞부분을 같이 배워보았습니다. 설명을 조금 자세히 하려고 해서 내용이 조금 길어진 것 같은데, 현상학적 방정식 설명한 부분은 제가 중간에 요약한 부분만 알면 되겠습니다. 그리고 제가 조금 귀찮아서(...) 문자에 대한 부연 설명을 덧붙여놓지 않은 게 많은데요, 혹시 너무 많이 없어서 식 이해하는 게 조금 어려웠다 하시는 분들 있으면 댓글로 알려주시면 좋을 것 같아요! 이런 분들이 많으시면 다음 글부터는 좀 더 하나하나 설명을 달도록 하겠습니다.
다음 글에서는 오늘 설명한 diffusivity, thermal conductivity, viscosity를 구하는 식을 유도해볼 것인데요, 이게 화학인지 수학인지 싶게 수식이 다수 등장할 예정입니다... 내용을 설명하는 데 테일러 급수가 사용될 예정이니, 물론 간단하게 설명을 덧붙이긴 하겠지만 잘 모르시는 분들은 미적분학 책에서 테일러 급수 내용 한 번 읽고 오시는 게 도움이 될 것이라 생각합니다. 그럼 이번 글은 이 정도에서 마치도록 하죠. 감사합니다!!
다음 글 보러 가기: https://susiljob.tistory.com/97