[Atkins' PHYSICAL CHEMISTRY] 16A.2 The transport parameters

안녕하세요! 수학은제친구가잘해요 입니다!! 시험 끝나고 여유가 조금 생겨서 열심히 연재하려고 합니다 ㅎㅎ 11월 둘째 주 정도까지 FOCUS 16 내용이 끝났으면 좋겠는데 가능할지는 잘 모르겠지만, 열심히 글 올려볼게요! 오늘 배울 내용은 저번 글에서 말한 바와 같이 diffusivity, thermal conductivity, viscosity를 계산하는 식을 구하고 각각 압력, 온도, 분자량에 따라 값이 어떻게 달라지는지 알아보겠습니다. 그리고 effusion과 관련하여 매우 낮은 증기 압력을 구하는 방법인 Knudsen method에 대해서도 간단히 배워볼게요. 글이 조금 길어질 것 같은데... 저번 글에서 내용을 전개한 방식과 비슷하게, diffusivity 구하는 방식이랑 나머지 구하는 방식이 유사합니다! 하나 이해하시면 나머지도 금방 이해하실 수 있을 거에요 ㅎㅎ 그럼 시작해보겠습니다!

 

이전 게시글 목록입니다.

• https://susiljob.tistory.com/89 (1B.1(a) Pressure and molecular speed)
• https://susiljob.tistory.com/90 (1B.1(b) The Maxwell-Boltzmann distribution of speed)
• https://susiljob.tistory.com/93 (1B.1(c) Mean values & 1B.2 Collisions)
• https://susiljob.tistory.com/95 (16A.1 The phenomenological equations (+ collision flux))

---

16A.2 The transport parameters

일단 저번 글에서 깜빡하고 설명하지 않은 것부터 설명해야겠네요... collision flux의 변수 의존성부터 언급하고 넘어가겠습니다. collision flux의 식은 저번 글에서 구해보았습니다.

$$ Z_W = \frac{p}{(2\pi m k_B T)^{\frac{1}{2}}} = \frac{p N_A}{(2\pi M R T)^{\frac{1}{2}}} = \frac{1}{4} \rho_{N} \left< v\right> $$

압력 의존성은 쉽게 볼 수 있네요. 온도가 일정하면 collision flux와 압력이 서로 비례하는 관계를 가진다는 것을 바로 구할 수 있어요. 기체의 압력은 기체가 용기 벽면을 때림으로써 발생하는 것이니까 collision flux와 비례하는 관계를 가진다고 생각해볼 수도 있을 것 같아요. ($ Z_W \propto p \ when \ const.T$)

 

기체의 분자량도 살펴보면, collision flux와 기체의 분자량의 제곱근이 반비례하는 관계를 가짐을 바로 알 수 있습니다. 기체의 분자량이 커지면 기체의 평균 속도가 내려가기 때문에($ \left< v\right> = (\frac{8RT}{\pi M})^{\frac{1}{2}} $), 기체가 벽면을 때리는 횟수도 줄어들 거에요. ($ Z_W \propto \frac{1}{M^{\frac{1}{2}}} $)

 

온도 의존성은 조금 조심해야 하는데요, 저 식만 보면 collision flux와 온도의 제곱근이 서로 반비례하는 관계를 가진다고 생각할 수 있겠습니다. 그러나 이는 압력이 일정한 경우에서만 성립합니다. 이상 기체 방정식에 의해 기체 몰수와 부피가 일정하면 압력과 온도가 서로 비례하는 관계를 가지기 때문에, 만약 온도가 4배 증가한다면 위의 식 우변의 분모는 2배, 분자는 4배 증가하게 되겠습니다. 즉 좌변은 2배 증가하게 되겠죠? 따라서 "일정 부피 조건"이 있다면 collision flux와 온도의 제곱근이 "비례"하게 되겠습니다. ($ Z_W \propto T^{\frac{1}{2}} \ when \ const.n \ and \ V $)

 

그리고 한 가지만 더 설명하고 넘어갈게요..! 책에는 나와 있지 않은데, 이해를 돕기 위해 "Mean collision distance from a plane"이라는 개념을 도입해보겠습니다. 기호는 $ l $을 사용할 거고요, 의미는 '벽에 충돌 전 가장 마지막으로 기체 분자와 충돌한 지점'으로부터 벽까지의 거리입니다. 그림을 통해 쉽게 이해하실 수 있는 개념인데요, 왼쪽에 빨간 화살표의 길이의 평균이 바로 $ l $입니다. 이 값은 mean free path랑 관련이 있어(1B.2 Collisions 참고) $ l=\frac{2}{3}\lambda $가 성립한다고 합니다. 왜 그런지는 잘 모르겠어요... 그냥 그렇구나 하고 넘어가겠습니다.

(a) The diffusion coefficient

이제 드디어! diffusivity를 어떻게 구할 수 있는지 알아보겠습니다! 3개 전부 유사한 방식으로 구해볼 건데요, collision flux를 이용하여 matter flux, energy flux, momentum flux를 구한 뒤 저번 시간에 말했던 현상학적 방정식과 동일하다고 하고 구할 것입니다. 저번 시간에도 말했듯 테일러 급수가 활용될 텐데, 간단히만 설명하고 넘어가겠습니다.

 

테일러 급수는 삼각함수, 지수함수, 로그함수 등 우리가 다루기 힘들어하는(?) 함수를 다항함수 꼴로 만드는 급수라고 생각하시면 됩니다. 일변수함수 $ f(x) $에 대해 이 함수가 무한 번 미분가능하다면 다음이 성립합니다.

$$ f(x+\Delta x) = \sum_{n=0}^{\infty}\frac{1}{n!}f^{(n)}(x)(\Delta x)^{n} = f(x)+f'(x)\Delta x + \frac{1}{2!}f''(x)(\Delta x)^2 +\cdots $$

이렇게 되는 이유는 설명하지 않을 거고요, 알고 싶으신 분은 미적분학 책에서 찾아보시면 되겠습니다. (되게 무책임한 발언 같네요...)

 

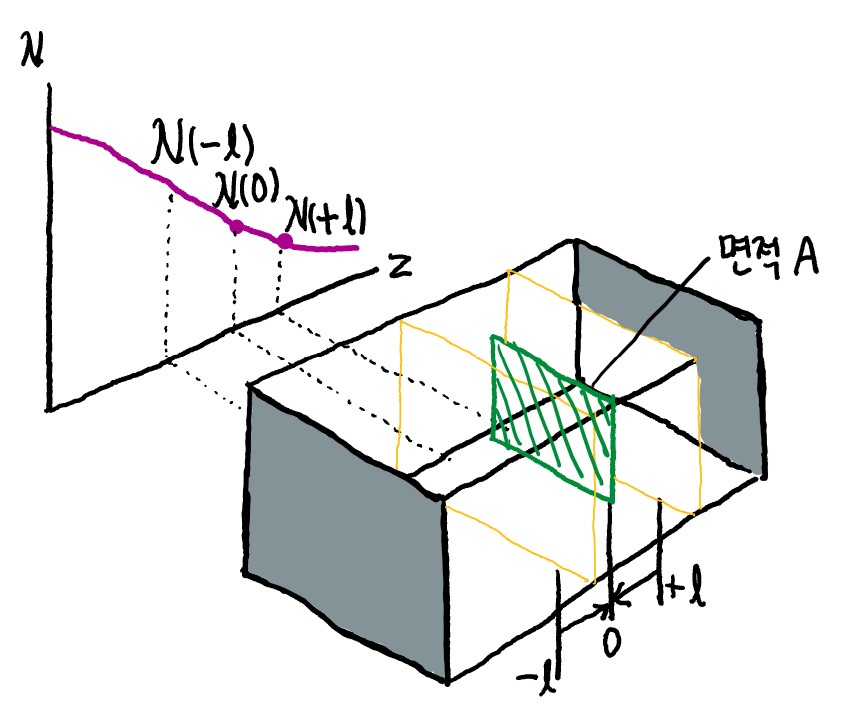
왼쪽 그림에서 number density가 z에 대한 함수임을 알 수 있는데요, 이 함수가 미분가능하다면 다음이 성립할 것입니다.

$$ \rho_N(z)\approx \rho_N(0)+z\frac{\mathrm{d} \rho_N(z)}{\mathrm{d} z}_{z=0} $$

계산의 편의를 위해 이차 이상의 항은 생략하도록 하겠습니다. 이제 z 자리에 $ \pm l $을 넣어보면 다음과 같은 식이 나오겠네요.

$$ \rho_N(\pm l)= \rho_N(0)+(\pm l)\frac{\mathrm{d} \rho_N(z)}{\mathrm{d} z}_{z=0} $$

 

이제 z=0에서의 matter flux, 정확히는 molecular flux를 구해보겠습니다. flux는 '알짜 양'이기 때문에, 양방향에서 오는 기체 분자를 한꺼번에 고려해주어야 해요. 따라서 z=0에서의 molecular flux는 (그림 기준으로) (왼쪽에서 오는 분자 수) - (오른쪽에서 오는 분자 수)를 고려하여 계산해야 합니다.

$$ J_{z=0}=J_{L\to R}-J_{R\to L} $$

 

이제 각 방향별로 flux를 구해줘야 하겠습니다. 이때, molecular flux의 절댓값은 그 지점에서의 collision flux와 같을 것입니다. 어떤 면을 지나는 분자는 당연히 그 면과 충돌을 하겠죠? 저번 시간에 collision flux 설명할 때 가상의 면에 대해서도 성립한다고 언급한 적이 있습니다. 따라서 다음의 수식이 성립할 거에요.

$$ J_{L\to R} = Z_{W}(-l) = \frac{1}{4} \rho_N (-l) \left< v\right> = \frac{1}{4} \left< v\right> (\rho_N(0) + (-l)\frac{\mathrm{d} \rho_N(z)}{\mathrm{d} z}_{z=0} \ ) $$

$$ J_{R\to L} = Z_{W}(+l) = \frac{1}{4} \rho_N (+l) \left< v\right> = \frac{1}{4} \left< v\right> (\rho_N(0) + (+l)\frac{\mathrm{d} \rho_N(z)}{\mathrm{d} z}_{z=0} \ ) $$

 

따라서 z=0 지점에서의 molecular flux는 위의 식에서 아래의 식을 빼서 구할 수 있겠네요.

$$ J_{z=0} = -\frac{1}{2} \left< v\right> l \frac{\mathrm{d} \rho_N(z)}{\mathrm{d} z}_{z=0} \ , J = -\frac{1}{2} \left< v\right> l \frac{\mathrm{d} \rho_N(z)}{\mathrm{d} z} $$

z=0만 빼면 바로 molecular flux 식이 나오게 되겠습니다. 근데 저번 시간에 우리는 $ J = -D \frac{\mathrm{d} \rho_N(z)}{\mathrm{d} z} $임을 배웠죠? 당연히 이 식과 위에서 구한 식은 동일합니다. 그리고 글 앞에서 $ l=\frac{2}{3}\lambda $라고 했으니 결론적으로 diffusivity는 다음의 식으로 구할 수 있습니다.

$$ D = \frac{1}{2} \left< v\right> l = \frac{1}{3} \left< v\right> \lambda $$

앳킨스 물리화학 책에서는 처음에 mean free path인 $ \lambda $를 사용하여 계산한 다음, 아까 설명드린 mean collision distance from a plane을 고려하여 보정하는 방식으로 식을 산출합니다. 제가 설명한 방식은 이를 먼저 고려한 것이니 사실 제 설명과 책의 설명은 완전히 동일하답니다! 헷갈릴 필요 없어요!

 

이제 압력, 온도, 분자량에 따라 값이 어떻게 달라지는지 알아볼게요! 1B.1(c)에서 구한 평균 속도 값($ \left< v\right> = (\frac{8RT}{\pi M})^{\frac{1}{2}} $), 1B.2(b)에서 구한 mean free path 식($ \lambda = \frac{k_B T}{\sigma p} $)까지 대입해보면 diffusivity는 다음의 식이 되겠습니다.

$$ D = \frac{1}{3} (\frac{8RT}{\pi M})^{\frac{1}{2}} \frac{k_B T}{\sigma p} $$

• 압력이 분모에 있으니 diffusivity와 압력은 반비례하는 관계입니다($ D \propto \frac{1}{p} $). 압력이 커지면 분자끼리의 충돌이 잦아져 분자가 특정 거리를 이동하는 데 더 오랜 시간이 걸릴 거에요.
• 그리고 분자량의 제곱근이 diffusivity와 반비례하겠네요($ D \propto \frac{1}{M^{\frac{1}{2}}} $). 분자량이 커지면 평균 속도가 느려지니 확산이 더 어려워질 거에요.
• 온도는 전체적으로 보면 온도가 높아지면 diffusivity가 커진다는 걸 알 수 있습니다($ D \propto T^{\frac{3}{2}}$). 온도가 올라가면 평균 속도가 빨라지기 때문이죠.

 

(b) Thermal conductivity

이번에는 Thermal conductivity입니다! 설명하기 전에, 완전 기체의 분자들이 에너지를 전달하는 방식에 대해 먼저 알아보겠습니다. 이와 관련된 법칙으로 에너지 등분배 법칙(Energy equipartition theorem)이 있는데, 각 분자가 가지는 자유도마다 같은 에너지를 분배받는다는 법칙입니다. 말이 조금 어려운데, 다음 그림을 보시면 익숙하실 겁니다! (일반화학에서 열역학 다룰 때도 나오는 내용이거든요 ㅎㅎ)

 

다들 어딘가에서 보셨을 그림이라고 생각합니다! 온도가 낮은 경우(실온 정도면 낮은 온도로 생각해도 좋습니다) 분자는 병진 운동과 회전 운동을 하게 되는데요, 분자의 모양에 따라 그림에 써놓은 것과 같이 자유도가 달라지게 됩니다. 온도가 높아지게 되면 분자 내부에서 진동이 일어나면서 자유도가 더 증가하게 되는데, 좀 어려워서 기초 물리화학 수준에서 잘 다루지 않아요.

 

에너지 등분배 법칙에 따르면, 분자들은 각 자유도마다 $ \frac{1}{2}k_{B}T $ 만큼의 에너지를 분배받게 됩니다. $ \nu $를 (자유도)/2 로 정의하게 되면, 하나의 분자는 온도 T에서 $ \varepsilon = \nu k_{B}T $만큼의 에너지를 가지게 됩니다.

 

이제 Thermal conductivity를 구해볼 거에요! 아까는 number density가 z에 대한 함수였다면, 이번에는 온도 T가 z에 대한 함수로 정의되겠습니다. 온도 기울기에 따라서 열이 이동할 테니까요! 그렇다면 T를 z에 대해서 테일러 전개를 해볼 수 있겠네요. 이번에도 일차항까지만 적어보겠습니다.

$$ T(\pm l)= T(0)+(\pm l)\frac{\mathrm{d} T(z)}{\mathrm{d} z}_{z=0} $$

그리고 계산의 편의를 위해 몇 가지 가정을 해볼 건데요, l(Mean collision distance from a plane)이 충분히 작아서 우리가 고려할 범위 안에서 number density와 온도가 일정하다고 가정해보겠습니다. 이렇게 되면 $ Z_W = \frac{1}{4} \rho_{N} \left< v\right> $의 값이 일정하게 될 거에요(평균 속도가 온도에 대한 함수니까요). 

 

그리고 아까처럼 $ J_{z=0}=J_{L\to R}-J_{R\to L} $가 될 텐데, 이때 J는 energy flux가 되겠죠. 다음의 식을 한 번 볼까요?

$$ J_{energy}=\frac{energy}{area \times time} = \frac{number\ of\ molecules}{area \times time} \times \frac{energy}{one\ molecule} = J_{molecule}\times \varepsilon $$

따라서 energy flux는 molecular flux와 한 분자가 가지는 에너지를 곱한 값과 동일합니다. 조금 전에 molecular flux와 collision flux를 동일하게 생각했으니, 아까처럼 다음이 성립할 거에요.

$$ J_{L \to R} = Z_{W} \varepsilon(-l) = Z_{W} \nu k_{B} T(-l) = Z_{W} \nu k_{B} (T(0) - l \frac{\mathrm{d} T(z)}{\mathrm{d} z}_{z=0}) $$

$$ J_{R \to L} = Z_{W} \varepsilon(+l) = Z_{W} \nu k_{B} T(+l) = Z_{W} \nu k_{B} (T(0) + l \frac{\mathrm{d} T(z)}{\mathrm{d} z}_{z=0}) $$

$$ J = -2 Z_{W} \nu k_{B} l \frac{\mathrm{d} T(z)}{\mathrm{d} z} = -2 (\frac{1}{4} \rho_{N} \left< v\right>) \nu k_{B} (\frac{2}{3} \lambda) \frac{\mathrm{d} T(z)}{\mathrm{d} z} = -\frac{1}{3} \nu k_{B} \left< v\right> \lambda \rho_{N} \frac{\mathrm{d} T(z)}{\mathrm{d} z} $$

 

이때 $ J = - \kappa \frac{\mathrm{d} T(z)}{\mathrm{d} z} $이므로, Thermal conductivity는 다음의 식으로 구할 수 있겠습니다.

$$ \kappa = \frac{1}{3} \nu k_{B} \left< v\right> \lambda \rho_{N} $$

그리고 $ D = \frac{1}{3} \left< v\right> \lambda $, $ \rho_{N} = \frac{p}{k_{B}T} $이므로 다음과 같이 나타낼 수도 있습니다.

$$ \kappa = \frac{\nu p}{T}D $$

 

이제 압력, 온도, 분자량에 따라 어떻게 달라지는지 알아보겠습니다. $ \left< v\right> = (\frac{8RT}{\pi M})^{\frac{1}{2}} $, $ \lambda = \frac{1}{\sigma \rho_{N}} $을 대입해봅시다.

$$ \kappa = \frac{1}{3} \nu k_{B} (\frac{8RT}{\pi M})^{\frac{1}{2}} \frac{1}{\sigma} $$

• 압력은 기본적으로 영향을 주지 않는다는 것을 알 수 있습니다. mean free path($ \lambda $)와 number density($ \rho_{N} $)가 서로 그 영향을 상쇄하기 때문인데요, 만약 압력이 매우 낮아 mean free path가 용기(container)의 사이즈보다 더 커지게 되면 mean free path 값이 의미가 없어지게 됩니다. 그리고 number density가 압력과 비례하니 thermal conductivity와 압력이 비례하게 될 것입니다.
• 분자량의 제곱근과 thermal conductivity가 서로 반비례하는데요($ D \propto \frac{1}{M^{\frac{1}{2}}} $), 에너지 전달의 매개체인 완전 분자의 속도가 느려져서 에너지 전달이 더 느려지게 됩니다.
• 온도의 제곱근과 thermal conductivity가 비례할 텐데($ D \propto T^{\frac{1}{2}} $), 이것도 평균 속도와 관련이 있습니다. 온도가 더 높으면 분자가 더 빠르게 움직일 테니까요.

 

(c) Viscosity

이제 viscosity입니다. 앞에서 했던 것들이랑 비슷하니까 빠르게 설명해볼게요! 이번에는 x 방향 속도가 z에 대한 함수로 주어질 것입니다. 따라서 다음과 같이 테일러 전개를 진행할 수 있겠네요.

$$ v_x(\pm l)= v_x(0)+(\pm l)\frac{\mathrm{d} v_x(z)}{\mathrm{d} z}_{z=0} $$

또한 momentum flux는 molecular flux와 선운동량(linear momentum, $mv_x$)의 곱으로 나타낼 수 있습니다.

$$ J_{momentum}=\frac{momentum}{area \times time} = \frac{number\ of\ molecules}{area \times time} \times \frac{momentum}{one\ molecule} = J_{molecule}\times mv_x $$

 

계산 과정을 조금 건너 뛰고, 다음의 식을 얻어낼 수 있습니다. 과정은 위와 거의 동일하니 스스로 해보실 수 있을 거에요!

$$ J_{momentum} = - \frac{1}{3} \left< v\right> \lambda m \rho_{N} \frac{\mathrm{d} v_x(z)}{\mathrm{d} z} $$

이때 $ J_{momentum} = - \eta \frac{\mathrm{d} v_x(z)}{\mathrm{d} z} $이므로 viscosity는 다음과 같습니다.

$$ \eta = \frac{1}{3} \left< v\right> \lambda m \rho_{N} $$

 

이때 $ D = \frac{1}{3} \left< v \right> \lambda $, $ \rho_{N} = \frac{nN_{A}}{V} = c N_{A} $, $ m = \frac{M}{N_A} $ 이므로 다음도 성립합니다.

$$ \eta = D m \rho_{N} = D c M $$

이외에도 책에 나온 것처럼 다양하게 식을 바꿀 수 있을 것 같습니다.

 

압력, 온도, 분자량에 대한 의존성만 보면 되겠습니다! 다시 식을 가져와서 $ \left< v\right> = (\frac{8RT}{\pi M})^{\frac{1}{2}} $, $ \lambda = \frac{1}{\sigma \rho_{N}} $을 대입하면 다음의 식이 나옵니다.

$$ \eta = \frac{1}{3} (\frac{8mk_{B}T}{\pi})^{\frac{1}{2}}\frac{1}{\sigma} $$

계산을 조금 건너뛰었는데, 어떻게 이 식이 나오는지는 그렇게 중요하지 않으니까 괜찮습니다...ㅎ

• p가 식에 없으니 압력은 viscosity에 영향을 주지 못합니다. Thermal conductivity의 경우처럼 mean free path와 number density가 압력 효과를 서로 상쇄하기 때문이죠.
• 온도의 제곱근과 viscosity가 서로 비례하는 것을 알 수 있습니다($ \eta \propto T^{\frac{1}{2}} $).
• diffusivity, thermal conductivity와 다르게, 분자량의 제곱근과 viscosity는 서로 '비례'하네요($ \eta \propto M^{\frac{1}{2}} $). 운동량=mv인 것을 생각해보면 그럴 듯하죠?

viscosity에 대해서는 부가적인 설명을 하나만 더해보겠습니다. viscosity가 momentum flux와 비례하는 값이기 때문에, viscosity가 커진다는 것은 운동량을 더 잘 전달한다는 것을 저번 시간에 배웠는데요. 기체 분자 사이에서는 운동량을 전달할 방법이 서로 충돌하는 것밖에 없습니다. 완전 기체를 가정하기 때문에 다른 방식으로는 기체 분자에게 영향을 줄 수 없기 때문입니다. 따라서 온도가 높아지면 더 충돌이 잦아지고, 운동량을 더 많이 전달하게 되는 것이므로 viscosity가 증가한다고 해석할 수 있습니다.

액체의 운동량 전달 방법은 기체와 다른데, 이에 대해서는 다음 글에서 다루도록 하겠습니다.

 

(d) Effusion

마지막으로 effusion입니다! 이건 어렵지 않아요. 만약 기체 분자들이 분출하는 구멍의 단면적이 $ A_{0} $라고 하면, 그 단면적과 충돌하는 분자들이 구멍을 통해 빠져나올 테니, 분출 속도는 다음과 같습니다.

$$ rate \ of \ effusion = Z_{W}A_{0} = \frac{p N_A A_0}{(2\pi M R T)^{\frac{1}{2}}} $$

저번 시간에 잠깐 배웠던 Graham's law of effusion에서 설명한 바(분출 속도는 분자량의 제곱근에 반비례)가 성립합을 알 수 있겠습니다. 이것도 압력과 온도에 따라 어떻게 달라지는지 알아보고 가겠습니다.

• 압력이 분출 속도와 비례함을 바로 알 수 있겠습니다. 압력이 커지면 구멍의 단면적에 충돌하는 분자 수가 늘어날 테니까요.
• 온도의 경우는 collision flux와 같이 상황을 나눠서 생각해야 합니다. collision flux와 마찬가지로 압력이 일정하면 온도의 제곱근과 분출 속도가 반비례하겠지만, 부피와 몰수가 일정하면 온도의 제곱근과 분출 속도가 비례합니다.

Knudsen method는 이 식을 이용하여 증기 압력을 계산하는 방법인데요, 다음 그림을 한 번 보시죠.

간단한 그림이죠? 작게 구멍이 뚫려 있는 용기에 끓는점이 높은 액체를 담고, 온도 T에서 이 액체의 증기 압력을 구하고자 합니다. 구하는 방법도 꽤 간단한데요, 일정 온도 상황에서 특정 시간이 지난 후에 액체의 질량 차이를 구하는 것입니다. 액체의 분자량을 알면 분출 속도를 구할 수 있겠죠? 이미 분출 속도 식에서 압력을 제외하고 나머지 값도 모두 알고 있으니, 단순하게 대입하면 증기 압력을 어렵지 않게 구할 수 있습니다.

 

 

 

---

글이 정말정말 많이 길어졌네요... 내용도 지금까지 다뤘던 내용 중에 가장 어려웠습니다 ㅠㅠ 글 쓰는 것도 가장 오래 걸리고 힘들었네요 ㅠㅠ... 위 내용을 전부 머릿속에 담는 것은 어렵기 때문에 간단하게 다시 정리해보겠습니다.

• collision flux는 충돌 횟수에 대한 flux를 말합니다. 압력이 높아지거나 분자량이 작아지면 collision flux가 커지고, 압력이 일정할 때는 온도가 높아지면 collision flux가 작아지는데, 부피가 일정할 때 온도가 높아지면 collision flux가 커집니다.
• diffusivity(확산계수), thermal conductivity(열 전도율), viscosity(점도)는 각각 number density(개수밀도), 온도, x 방향 속도를 z 방향에 대한 테일러 전개로 나타내어 구한 flux와 현상학적 방정식의 flux가 동일하다고 하고 구합니다.
• diffusivity는 $ D = \frac{1}{3} \left< v\right> \lambda $입니다. 압력과 분자량이 높아지면 diffusivity가 작아지고 온도가 높아지면 diffusivity는 커집니다.
• thermal conductivity는 $ \kappa = \frac{1}{3} \nu k_{B} \left< v\right> \lambda \rho_{N} $입니다. 압력은 영향을 주지 못하고, 분자량이 작아지거나 온도가 높아지면 thermal conductivity가 커집니다.
• viscosity는 $ \eta = \frac{1}{3} \left< v\right> \lambda m \rho_{N} $입니다. 압력은 영향을 주지 못하고, 분자량이 커지거나 온도가 높아지면 viscosity는 커집니다.
• $ rate \ of \ effusion = Z_{W}A_{0} = \frac{p N_A A_0}{(2\pi M R T)^{\frac{1}{2}}} $입니다. 분출 속도와 관련하여, 일정 온도에서 특정 시간동안 액체 or 고체의 질량 변화를 측정하여 증기 압력을 측정하는 Knudsen method가 있습니다.

요약하자면 위와 같습니다. 식이 도출되는 자세한 방식을 알고 직접 해보는 것도 중요하지만, 각각의 식을 알고 있는 것도 중요합니다. 글 내용이 많고 어렵기 때문에, 먼저 요약한 바를 이해한 후에 세부적인 것을 알아보는 것도 좋습니다.

 

다음 글에서는 액체 분자의 운동에 대해서 알아볼 것입니다. 오늘 내용도 어려웠지만, 개인적으로 다음 글에서 다룰 내용이 더 어렵다고 느꼈습니다 ㅠㅠㅠ 두 번으로 나눠서 연재할 거라서 분량은 조금 줄어들겠지만, 식을 하나하나 이해해야 하는 과정이 조금 더 어렵기 때문에 마음 단단히 먹으셔야 할 겁니다 ㅋㅋ! 그럼 다음 글에서 뵙겠습니다. 감사합니다!

 

다음 글 보러 가기: https://susiljob.tistory.com/124